题目内容
若lgx,lg(x-2y),lgy三个数成等差数列,则 的值是
的值是
- A.1
- B.4
- C.

- D.1或4
B
分析:由lgx,lg(x-2y),lgy三个数成等差数列,根据等差数列的性质列出关系式,利用对数的运算性质化简得到关于x与y的关系式,在关系式两边同时除以y2,得到关于 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到 的值.
的值.
解答:∵lgx,lg(x-2y),lgy三个数成等差数列,
∴2lg(x-2y)=lgx+lgy,即(x-2y)2=xy,
整理得:x2-5xy+4y2=0,
等号两边同时除以y2得:( )2-5•
)2-5• +4=0,
+4=0,
解得: =4或
=4或 =1,
=1,
又x>0,y>0,且x-2y>0,
∴ >2,
>2,
则 的值是4.
的值是4.
故选B
点评:此题考查了等差数列的性质,对数的运算法则,以及一元二次方程的解法,熟练掌握等差数列的性质是解本题的关键,同时注意根据对数的真数大于0,舍去1,得到满足题意的解.
分析:由lgx,lg(x-2y),lgy三个数成等差数列,根据等差数列的性质列出关系式,利用对数的运算性质化简得到关于x与y的关系式,在关系式两边同时除以y2,得到关于
 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到 的值.
的值.解答:∵lgx,lg(x-2y),lgy三个数成等差数列,
∴2lg(x-2y)=lgx+lgy,即(x-2y)2=xy,
整理得:x2-5xy+4y2=0,
等号两边同时除以y2得:(
 )2-5•
)2-5• +4=0,
+4=0,解得:
 =4或
=4或 =1,
=1,又x>0,y>0,且x-2y>0,
∴
 >2,
>2,则
 的值是4.
的值是4.故选B
点评:此题考查了等差数列的性质,对数的运算法则,以及一元二次方程的解法,熟练掌握等差数列的性质是解本题的关键,同时注意根据对数的真数大于0,舍去1,得到满足题意的解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的值是( )
的值是( )
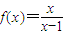 ,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;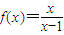 ,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;