题目内容

已知M={(a+3)+(b2-1)i,8},N={3i,(a2-1)+(b+2)i},同时满足M∩NM,M∩N≠,求整数a、b.?

思路分析:利用集合关系,建立复数之间的等量关系,再利用复数相等的定义,将复数问题转化为实数问题即可求解.

解:依题意得(a+3)+(b2-1)i=3i或(a2-1)+(b+2)i=8或(a+3)+(b2-1)i=(a2-1)+(b+2)i.?

由(a+3)+(b2-1)i=3i,得a=-3,b=±2.??

经检验,a=-3,b=-2不合题意,舍去.?

∴a=-3,b=2.?

由(a2-1)+(b+2)i=8,得a=±3,b=-2;?

又a=-3,b=-2不合题意,?

∴a=3,b=-2.?

由(a+3)+(b2-1)i=(a2-1)+(b+2)i,?

得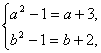

从而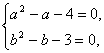

解得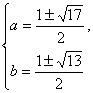 (舍去).??

综上所述,a=-3,b=2或a=3,b=-2.

练习册系列答案
相关题目
已知M（-3，0）﹑N（3，0），P为坐标平面上的动点，且直线PM与直线PN的斜率之积为常数m（m≥-1，m≠0）．
（1）求P点的轨迹方程并讨论轨迹是什么曲线？
（2）若m=-
5
9
，P点的轨迹为曲线C，过点Q（2，0）斜率为k1的直线?1与曲线C交于不同的两点A﹑B，AB中点为R，直线OR（O为坐标原点）的斜率为k2，求证k1k2为定值；
（3）在（2）的条件下，设
QB
=λ
AQ
，且λ∈[2，3]，求?1在y轴上的截距的变化范围．
已知向量
a
=(
3
，k)，
b
=（0，-1），
c
=(1，
3
)．
（Ⅰ）若
a
⊥
c
，求k的值；
（Ⅱ）当k=1时，
a
-λ
b
与
c
共线，求λ的值；
（Ⅲ）若|
m
|=
3
|
b
|，且
m
与
c
的夹角为150°，求|
m
+2
c
|
已知向量
a
=(
3
 ， cos2ωx) ，  
b
=(sin2ωx ，  1) ，  (ω＞0)，令f(x)=
a
•
b
，且f（x）的周期为π．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若x∈[0，
π
2
]时f（x）+m≤3，求实数m的取值范围．
已知M=(a+3)(a-5),N=(a+2)(a-4),则(    )

A.M＞N                                 B.M=N

C.M＜N                                 D.M、N的大小关系不能确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网