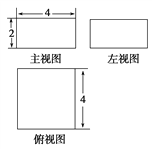
题目内容
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() 的中点.
的中点.
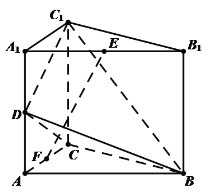
(1)求证:![]() ∥平面
∥平面![]()
(2)若异面直线![]() 与
与![]() 所成角为
所成角为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]()
【解析】
分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() , ,由棱柱的性质可得
, ,由棱柱的性质可得![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,,再由面面平行的判定得到平面平面
,,再由面面平行的判定得到平面平面![]() ∥平面
∥平面![]() ,,则答案得到证明;
,,则答案得到证明;
(2)由(1)知知![]() 异面直线
异面直线![]() 与
与![]() 所成角,所以
所成角,所以![]() , ,进一步得到
, ,进一步得到![]() 平面
平面![]() ,,,再由已知求出
,,,再由已知求出![]() 的长度,把三棱锥
的长度,把三棱锥![]() 的体积转化为
的体积转化为![]() 的体积求解.
的体积求解.
详解:
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,

因为![]() 分别为棱
分别为棱![]() 的中点,所以
的中点,所以![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,
![]() ,同理可证
,同理可证![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,
所以平面![]() ∥平面
∥平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() .
.
(2)由(1)知![]() 异面直线
异面直线![]() 与
与![]() 所成角,所以
所成角,所以![]() ,
,
因为三棱柱![]() 为直三棱柱,所以
为直三棱柱,所以![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,
![]() .
.
![]()
![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
所以![]()
![]() .
.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
【题目】某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加书法社团 | 2 | 30 |
(1)从该班随机选 1 名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的 8 名同学中,有 5 名男同学![]() ,3名女同学
,3名女同学![]() .现从这 5 名男同学和 3 名女同学中各随机选 1 人,求
.现从这 5 名男同学和 3 名女同学中各随机选 1 人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.