题目内容
已知正项数列{an}的前n项和为Sn,3an为方程x2+2x-12Sn=0的一根(N∈n).
(1)求数列{an}通项公式an;
(2)求证:当N≥2时, +
+ +…+
+…+ <
< .
.
解:(1)∵原方程x2+2x-12Sn=0有一根为3an
∴9 即4
即4 …①…(1分)
…①…(1分)
令n=1,
∴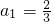 或a1=0
或a1=0
∵an>0
∴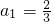 (2分)
(2分)
当n≥2时, …②
…②
①-②得:4 +2an-2an-1
+2an-2an-1
即(an+an-1)(an-an-1 )=0
)=0
∵an>0
∴an-an-1 =0…(5分)
=0…(5分)
∴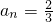
 =
= 满足
满足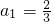
∴ …(6分)
…(6分)
(2)记Cn═
则Cn+1-Cn=


=[
 ]
] <0
<0
∴Cn>Cn+1…(9分)
∴Cn<Cn-1<Cn-2<…<C2
即Cn≤C2= =
= …(11分)
…(11分)
∴ +
+ +…+
+…+ =
= [
[ ]
]
= Cn
Cn ×
× =
=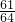
 =
= …(12分)
…(12分)
分析:(1)由已知可得,9 即4
即4 ,从而可求a1,利用an=Sn-Sn-1可得an-an-1
,从而可求a1,利用an=Sn-Sn-1可得an-an-1 =0,结合等差数列的通项公式可求
=0,结合等差数列的通项公式可求
(2)记Cn═ ,利用单调性的定义可判断Cn>Cn+1即Cn<Cn-1<Cn-2<…<C2,从而可得Cn≤C2,代入可证
,利用单调性的定义可判断Cn>Cn+1即Cn<Cn-1<Cn-2<…<C2,从而可得Cn≤C2,代入可证
点评:本题综合考查了数列的递推公式在数列的通项求解中的应用,等差数列的通项公式的求解及数列的单调性等知识的应用,试题具有一定的综合性
∴9
 即4
即4 …①…(1分)
…①…(1分)令n=1,

∴
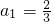 或a1=0
或a1=0∵an>0
∴
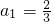 (2分)
(2分)当n≥2时,
 …②
…②①-②得:4
 +2an-2an-1
+2an-2an-1即(an+an-1)(an-an-1
 )=0
)=0∵an>0
∴an-an-1
 =0…(5分)
=0…(5分)∴
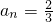
 =
= 满足
满足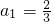
∴
 …(6分)
…(6分)(2)记Cn═

则Cn+1-Cn=



=[

 ]
] <0
<0∴Cn>Cn+1…(9分)
∴Cn<Cn-1<Cn-2<…<C2
即Cn≤C2=
 =
= …(11分)
…(11分)∴
 +
+ +…+
+…+ =
= [
[ ]
]=
 Cn
Cn ×
× =
=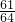
 =
= …(12分)
…(12分)分析:(1)由已知可得,9
 即4
即4 ,从而可求a1,利用an=Sn-Sn-1可得an-an-1
,从而可求a1,利用an=Sn-Sn-1可得an-an-1 =0,结合等差数列的通项公式可求
=0,结合等差数列的通项公式可求(2)记Cn═
 ,利用单调性的定义可判断Cn>Cn+1即Cn<Cn-1<Cn-2<…<C2,从而可得Cn≤C2,代入可证
,利用单调性的定义可判断Cn>Cn+1即Cn<Cn-1<Cn-2<…<C2,从而可得Cn≤C2,代入可证点评:本题综合考查了数列的递推公式在数列的通项求解中的应用,等差数列的通项公式的求解及数列的单调性等知识的应用,试题具有一定的综合性

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目