题目内容

设数列{an}是首项为1的正项数列，且（n+1）a2n+1-na2n+an+1an=0（n=1，2，3，…）。
（1）求{an}的通项公式；
（2）设f（x）=xln（1+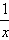），试判断f（x）在（0，+∞）上的单调性；
（3）设bn=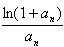，证明：ln2≤bn＜ln3。

解：（1）
得
∴
∴

∵时，
∴。
（2）∵
设x>0，令则t>0
∴，且
∵t>0，若g'（t）＜0，则
令
则
∴h（t）在（0，+∞）上为增函数，
∴h（t）>h（0）=0
∴g'（t）＜0在（0，+∞）上恒成立
从而在（0，+∞）上是增函数。
（3）∵
设
则



∴。
练习册系列答案
相关题目
设数列{an}是首项为1公比为3的等比数列，把{an}中的每一项都减去2后，得到一个新数列{bn}，{bn}的前n项和为Sn，对任意的n∈N*，下列结论正确的是（　　）
A、bn+1=3bn，且Sn=
1
2
（3n-1）
B、bn+1=3bn-2，且Sn=
1
2
（3n-1）
C、bn+1=3bn+4，且Sn=
1
2
（3n-1）-2n
D、bn+1=3bn-4，且Sn=
1
2
（3n-1）-2n
设数列{an}是首项为0的递增数列，fn(x)=|sin
1
n
(x-an)|，x∈[an，an+1](n∈N*)，满足：对于任意的b∈[0，1），fn（x）=b总有两个不同的根，则{an}的通项公式为
an=
n(n-1)
2
π
an=
n(n-1)
2
π
．
设数列{an}是首项为1，公差为2的等差数列，对每一个k∈N*，在ak与ak+1之间插入2k-1个2，得到新数列{bn}，设An、Bn分别是数列{an}和{bn}的前n项和．
（1）a10是数列{bn}的第几项；
（2）是否存在正整数m，使Bm=2010？若不存在，请说明理由；否则，求出m的值；
（3）设am是数列{bn}的第f（m）项，试比较：Bf（m）与2Am的大小，请详细论证你的结论．
设数列{an}是首项为50，公差为2的等差数列；{bn}是首项为10，公差为4的等差数列，以ak、bk为相邻两边的矩形内最大圆面积记为Sk，若k≤21，那么Sk等于
（2k+3）2π
（2k+3）2π
．
（2013•广东）设数列{an}是首项为1，公比为-2的等比数列，则a1+|a2|+a3+|a4|=
15
15
．