题目内容
已知函数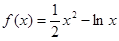 。
。
(Ⅰ)求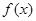 的单调区间;
的单调区间;
(Ⅱ)若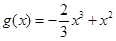 ,证明当
,证明当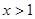 时,函数
时,函数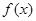 的图象恒在函数
的图象恒在函数 图象的上方.
图象的上方.
(Ⅰ)单调递减区间是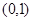 。单调递增区间是
。单调递增区间是 ;(Ⅱ)参考解析.
;(Ⅱ)参考解析.
解析试题分析:(Ⅰ)本小题含对数式的函数,首先确定定义域.通过求导就可知道函数的单调区间.本题的易错易漏点就是定义域的范围.(Ⅱ)函数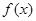 的图象恒在函数
的图象恒在函数 图象的上方等价于两个函数的对减后的值恒大于零(设在上方的减去在下方的).所以转化成在x>1上的恒大于零的问题.通过构造新的函数,对其求导,得到函数在x>1上为递增函数.又f(1)>0.所以函数恒大于零.即函数
图象的上方等价于两个函数的对减后的值恒大于零(设在上方的减去在下方的).所以转化成在x>1上的恒大于零的问题.通过构造新的函数,对其求导,得到函数在x>1上为递增函数.又f(1)>0.所以函数恒大于零.即函数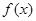 的图象恒在函数
的图象恒在函数 图象的上方成立.
图象的上方成立.
试题解析:解:(Ⅰ)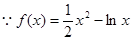 的定义域为
的定义域为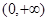 ,
,
又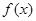 求得:
求得: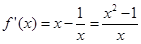 2分
2分
令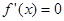 ,则
,则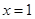 3分
3分
当 变化时,
变化时,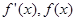 的变化情况如下表:
的变化情况如下表:
故
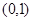
1 
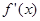
- 0 + 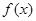
↘ 极小值 ↗ 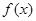 的单调递减区间是
的单调递减区间是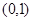 。单调递增区间是
。单调递增区间是 6分
6分
(Ⅱ)令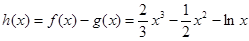
则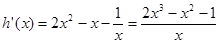
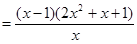 8分
8分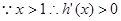
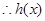 在
在 上单调递增 10分
上单调递增 10分
又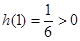
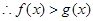
∴当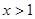 时,
时,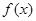 的图象恒在
的图象恒在 图象的上方. 12分
图象的上方. 12分
考点:1.含对数的函数的求导数.2.应用函数的单调性解决一些问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 个月顾客对某种商品的需求总量
个月顾客对某种商品的需求总量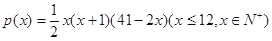 (单位:件)
(单位:件)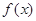 的表达式;
的表达式;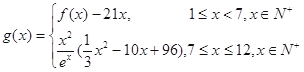 (单位:件),每件利润
(单位:件),每件利润 (单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据:
(单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据: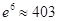 )
)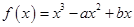 的图象与直线
的图象与直线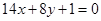 相切于点
相切于点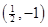 .
. 和
和 的值; (2)求
的值; (2)求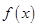 的极值.
的极值.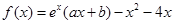 ,曲线
,曲线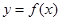 在点
在点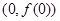 处切线方程为
处切线方程为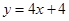 .
.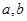 的值;
的值;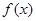 的单调性,并求
的单调性,并求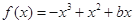 ,
,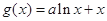 (
(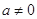 )
)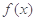 存在极值点,求实数b的取值范围;
存在极值点,求实数b的取值范围;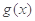 的单调区间;
的单调区间;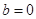 且
且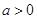 时,令
时,令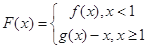 ,
,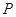 (
(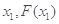 ),
),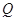 (
(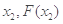 )为曲线y=
)为曲线y=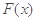 上的两动点,O为坐标原点,能否使得
上的两动点,O为坐标原点,能否使得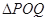 是以O为直角顶点的直角三角形,且斜边中点在y轴上?请说明理由
是以O为直角顶点的直角三角形,且斜边中点在y轴上?请说明理由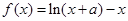 的最大值为0,其中
的最大值为0,其中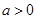 。
。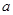 的值;
的值; 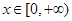 ,有
,有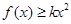 成立,求实数
成立,求实数 的最大值;
的最大值;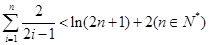
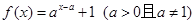 ,恒过定点
,恒过定点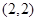 .
.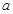 ;
;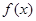 的图象向下平移1个单位,再向左平移
的图象向下平移1个单位,再向左平移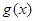 ,设函数
,设函数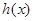 ,直接写出
,直接写出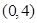 上的函数
上的函数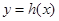 ,若在其定义域内,不等式
,若在其定义域内,不等式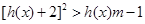 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.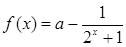 .
. 存在零点,求
存在零点,求 的取值范围
的取值范围 ,使
,使 为奇函数?如果存在,求
为奇函数?如果存在,求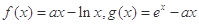 ,其中a为正实数.
,其中a为正实数.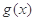 的极值点,讨论函数
的极值点,讨论函数 的单调性;
的单调性; 上无最小值,且
上无最小值,且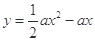 在
在