题目内容
以知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,过点
,过点![]() 的直线与椭圆相交与
的直线与椭圆相交与![]() 两点,且
两点,且![]() 。
。
(1) 求椭圆的离心率;
(2) 求直线AB的斜率;
(3) 设点C与点A关于坐标原点对称,直线![]() 上有一点
上有一点![]() 在
在![]()
![]() 的外接圆上,求
的外接圆上,求![]() 的值
的值
本小题主要考查椭圆的标准方程和几何性质、直线的方程、圆的方程等基础知识,考查用代数方法研究圆锥曲线的性质及数形结合的思想,考查运算能力和推理能力,
(I) 解:由![]() //
//![]() 且
且![]() ,得
,得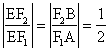 ,从而
,从而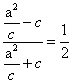
整理,得![]() ,故离心率
,故离心率![]()
![]()
(II) 解:由(I)得![]() ,所以椭圆的方程可写为
,所以椭圆的方程可写为![]()
设直线AB的方程为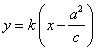 ,即
,即![]() .
. ![]()
![]()
由已知设![]() ,则它们的坐标满足方程组
,则它们的坐标满足方程组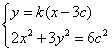
消去y整理,得![]() .
.
依题意,![]()
而 ![]() ①
①
![]() ②
②
由题设知,点B为线段AE的中点,所以
![]() ③
③
联立①③解得![]()
![]() ,
,![]()
将![]() 代入②中,解得
代入②中,解得![]() .
.
(III)解法一:由(II)可知![]()
当![]() 时,得
时,得![]() ,由已知得
,由已知得![]() .
.
线段![]() 的垂直平分线l的方程为
的垂直平分线l的方程为![]() 直线l与x轴
直线l与x轴
的交点![]() 是
是![]() 外接圆的圆心,因此外接圆的方程为
外接圆的圆心,因此外接圆的方程为![]() .
.
直线![]() 的方程为
的方程为![]() ,于是点H(m,n)的坐标满足方程组
,于是点H(m,n)的坐标满足方程组
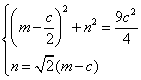 , 由
, 由![]() 解得
解得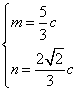 故
故![]()
当![]() 时,同理可得
时,同理可得![]() .
. ![]()
![]()
解法二:由(II)可知![]()
当![]() 时,得
时,得![]() ,由已知得
,由已知得![]()
由椭圆的对称性可知B,![]() ,C三点共线,因为点H(m,n)在
,C三点共线,因为点H(m,n)在![]() 的外接圆上,
的外接圆上,
且![]() ,所以四边形
,所以四边形![]() 为等腰梯形.
为等腰梯形.
由直线![]() 的方程为
的方程为![]() ,知点H的坐标为
,知点H的坐标为![]() .
.
因为![]() ,所以
,所以![]() ,解得m=c(舍),或
,解得m=c(舍),或![]() .
.
则![]() ,所以
,所以![]() .
.
当![]() 时同理可得
时同理可得![]()

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
F1、F2为椭圆的两个焦点,以F2为圆心作圆F2,已知圆F2经过椭圆的中心,且与椭圆相交于M点,若直线MF1恰与圆F2相切,则该椭圆的离心率e为( )
A、
| ||||
B、2-
| ||||
C、
| ||||
D、
|