题目内容
已知a1=9,点(an,an+1)在函数f(x)=x2+2x的图象上,其中n∈N*,设bn=lg(1+an).
(Ⅰ) 证明数列{bn}是等比数列;
(Ⅱ) 设cn=nbn,求数列{cn}的前n项和Sn;
(Ⅲ) 设dn=
+
,求数列{dn}的前n项和Dn.
(Ⅰ) 证明数列{bn}是等比数列;
(Ⅱ) 设cn=nbn,求数列{cn}的前n项和Sn;
(Ⅲ) 设dn=
| 1 |
| an |
| 1 |
| an+2 |
分析:(Ⅰ)把点的坐标代入函数解析式,两边同加1后取常用对数可得数列{bn}的递推式,由等比数列的定义可得结论;
(Ⅱ)由(Ⅰ)求出bn,进而得到cn,利用错位相减法可得Sn;
(Ⅲ)由an+1=
+2an,得an+1=an(an+2),取倒数可得到
=
-
,代入dn=
+
,得dn=2(
-
),由此可表示出Dn=2(
-
),由(1)知:lg(1+an)=2n-1,可求得an+1;
(Ⅱ)由(Ⅰ)求出bn,进而得到cn,利用错位相减法可得Sn;
(Ⅲ)由an+1=
| a | 2 n |
| 1 |
| an+2 |
| 1 |
| an |
| 2 |
| an+1 |
| 1 |
| an |
| 1 |
| an+2 |
| 1 |
| an |
| 1 |
| an+1 |
| 1 |
| a1 |
| 1 |
| an+1 |
解答:解:(Ⅰ) 证明:由题意知:an+1=
+2an,
∴an+1+1=(an+1)2,
∵a1=9∴an+1>0,
∴lg(an+1+1)=lg(an+1)2,即bn+1=2bn.
又∵b1=lg(1+a1)=1>0,
∴{bn}是公比为2的等比数列.
(Ⅱ) 由(1)知:bn=b1•2n-1=2n-1,∴cn=n•2n-1.
∴Sn=c1+c2+…+cn=1•20+2•21+3•22+…+n•2n-1①,
∴2Sn=1•21+2•22+3•23+…+(n-1)•2n-1+n•2n②,
∴①-②得,-Sn=1•20+21+22+…+2n-1-n•2n=
-n•2n=2n-1-n•2n,
∴S n=n•2n-2n+1.
(Ⅲ)∵an+1=
+2an=an(
+2)>0,
∴
=
(
-
),∴
=
-
,
∴dn=
+
-
=2(
-
),
∴Dn=d1+d2+…+dn=2(
-
+
-
+…
-
)=2(
-
),
又由(1)知:lg(1+an)=2n-1,
∴an+1=102n-1,∴an+1=102n-1,
∴Dn=2(
-
).
| a | 2 n |
∴an+1+1=(an+1)2,
∵a1=9∴an+1>0,
∴lg(an+1+1)=lg(an+1)2,即bn+1=2bn.
又∵b1=lg(1+a1)=1>0,
∴{bn}是公比为2的等比数列.
(Ⅱ) 由(1)知:bn=b1•2n-1=2n-1,∴cn=n•2n-1.
∴Sn=c1+c2+…+cn=1•20+2•21+3•22+…+n•2n-1①,
∴2Sn=1•21+2•22+3•23+…+(n-1)•2n-1+n•2n②,
∴①-②得,-Sn=1•20+21+22+…+2n-1-n•2n=
| 1-2n |
| 1-2 |
∴S n=n•2n-2n+1.
(Ⅲ)∵an+1=
| a | 2 n |
| a | n |
∴
| 1 |
| an+1 |
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| an+2 |
| 1 |
| an+2 |
| 1 |
| an |
| 2 |
| an+1 |
∴dn=
| 1 |
| an |
| 1 |
| an |
| 2 |
| an+1 |
| 1 |
| an |
| 1 |
| an+1 |
∴Dn=d1+d2+…+dn=2(
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 1 |
| an+1 |
| 1 |
| a1 |
| 1 |
| an+1 |
又由(1)知:lg(1+an)=2n-1,
∴an+1=102n-1,∴an+1=102n-1,
∴Dn=2(
| 1 |
| 9 |
| 1 |
| 102 n-1 |
点评:本题考查由数列递推公式求数列通项、数列求和、数列的函数特性,考查学生综合运用知识分析解决问题的能力,综合性较强,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.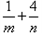 的最小值为
的最小值为