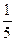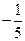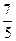题目内容
已知双曲线 的左、右顶点分别为A、B,双曲线在第一象限的图像上有一点P,
的左、右顶点分别为A、B,双曲线在第一象限的图像上有一点P, ,则
,则
A. B.
B.
C. D.
D.
 的左、右顶点分别为A、B,双曲线在第一象限的图像上有一点P,
的左、右顶点分别为A、B,双曲线在第一象限的图像上有一点P, ,则
,则A.
 B.
B.
C.
 D.
D.
A
根据题意可表示A,B坐标,设出P坐标,则可分别表示出PA和PB的斜率,二者乘求得 ,根据双曲线方程可知
,根据双曲线方程可知  =1,进而可推断出-tanαtanβ=1.
=1,进而可推断出-tanαtanβ=1.
解:A(-a,0),B(a,0),P(x,y),
kPA=tanα=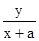 ,①
,①
kPB=-tanβ=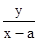 ,②
,②
由x2-y2=a2得 =1,
=1,
①×②,得-tanαtanβ=1,
故选A.
 ,根据双曲线方程可知
,根据双曲线方程可知  =1,进而可推断出-tanαtanβ=1.
=1,进而可推断出-tanαtanβ=1.解:A(-a,0),B(a,0),P(x,y),
kPA=tanα=
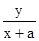 ,①
,①kPB=-tanβ=
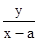 ,②
,②由x2-y2=a2得
 =1,
=1,①×②,得-tanαtanβ=1,
故选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 与
与
 ,其中
,其中 ,且
,且
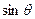 和
和 的值;
的值; ,求
,求 的值.
的值. 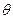 =" 2" ,求
=" 2" ,求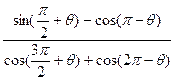 的值 .
的值 .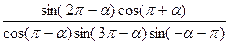 ;
; 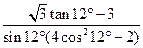 .
. ,
, ,则
,则 的值为 .
的值为 . ____________;
____________;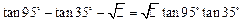 中,根号下的
中,根号下的 表示的正整数是____________.
表示的正整数是____________.  ,
, 为方程
为方程 的两个实根,
的两个实根, ,求
,求 及
及 的值.
的值.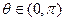 ,且
,且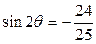 ,则
,则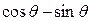 =
=