题目内容
已知定义在实数集 上的奇函数
上的奇函数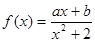 (
(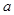 、
、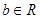 )过已知点
)过已知点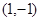 .
.
(Ⅰ)求函数的解析式;
(Ⅱ)试证明函数 在区间
在区间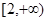 是增函数;若函数
是增函数;若函数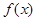 在区间
在区间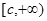 (其中
(其中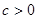 )也是增函数,求
)也是增函数,求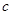 的最小值;
的最小值;
(Ⅲ)试讨论这个函数的单调性,并求它的最大值、最小值,在给出的坐标系(见答题卡)中画出能体现主要特征的图简;
(Ⅳ)求不等式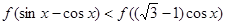 的解集.
的解集.
 上的奇函数
上的奇函数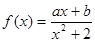 (
(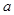 、
、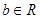 )过已知点
)过已知点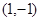 .
.(Ⅰ)求函数的解析式;
(Ⅱ)试证明函数
 在区间
在区间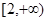 是增函数;若函数
是增函数;若函数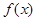 在区间
在区间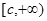 (其中
(其中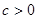 )也是增函数,求
)也是增函数,求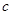 的最小值;
的最小值;(Ⅲ)试讨论这个函数的单调性,并求它的最大值、最小值,在给出的坐标系(见答题卡)中画出能体现主要特征的图简;
(Ⅳ)求不等式
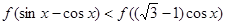 的解集.
的解集.(1)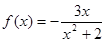 ;(2)用定义法证明,
;(2)用定义法证明,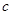 的最小值为
的最小值为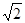 .(3)
.(3)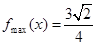 ,
,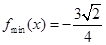 .(4)
.(4)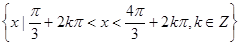 。
。
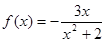 ;(2)用定义法证明,
;(2)用定义法证明,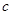 的最小值为
的最小值为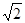 .(3)
.(3)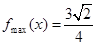 ,
,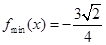 .(4)
.(4)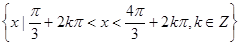 。
。试题分析:(1)由奇函数
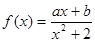 得
得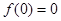 ,得
,得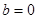 ,又过
,又过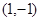 点得
点得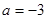 ;所以
;所以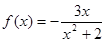 ,显然可以发现它是一个奇函数. (3分)
,显然可以发现它是一个奇函数. (3分)(2)设
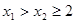 ,有
,有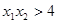 ,
,这样就有
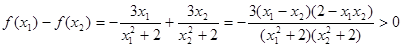 ,
,即函数
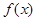 在区间
在区间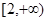 是增函数
是增函数对于函数
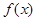 在区间
在区间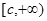 (
(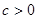 )也是增函数,
)也是增函数,设
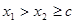 ,有
,有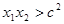 ;
;这样,欲使
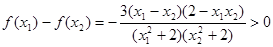 成立,
成立,须使
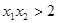 成立,从而只要
成立,从而只要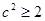 就可以,所以
就可以,所以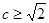 ,就能使函数
,就能使函数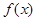 在区间
在区间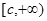 是增函数;
是增函数;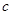 的最小值为
的最小值为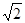 . (3分)
. (3分)(3)由(2)可知函数
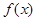 在区间
在区间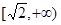 是增函数;
是增函数;由奇函数可知道,函数
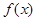 在区间
在区间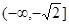 也是增函数;
也是增函数;那么,在区间
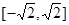 呢?设
呢?设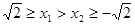 ,有
,有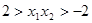 ;这样,就有
;这样,就有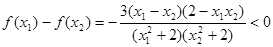 成立,即
成立,即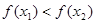 ,所以,函数
,所以,函数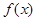 在区间
在区间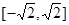 是减函数.
是减函数. 这样,就有
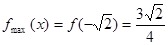 ,
,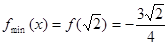 .
. 图像如下所示. (3分)
(4)因为
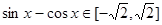 ,
,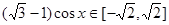 ,由(3)知道函数
,由(3)知道函数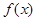 在区间
在区间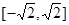 是减函数,这样,不等式
是减函数,这样,不等式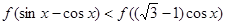 可以化为
可以化为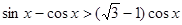 ,即
,即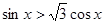 ;
; 它的解集为
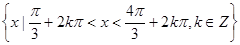 . (3分)
. (3分)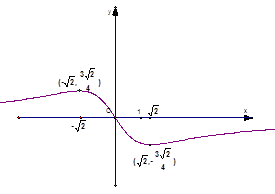
点评:(1)若f(x)是奇函数,且在x=0处有定义,则f(0)一定为0.(2)用定义法证明函数的单调性的步骤:一设二作差三变形四判断符号五得出结论,其中最重要的是四变形,最好变成几个因式乘积的形式,这样便于判断符号。(3)解
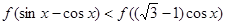 这类不等式的关键是根据函数的单调性脱去“f”号。
这类不等式的关键是根据函数的单调性脱去“f”号。
练习册系列答案
相关题目
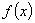 和偶函数
和偶函数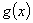 满足
满足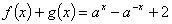
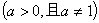 ,若
,若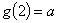 ,则
,则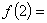
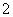
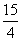
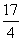
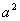
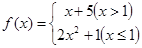 ,则
,则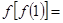 .
. 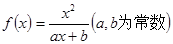 ,且方程
,且方程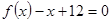 有两个实根
有两个实根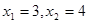 .
.  的解析式;
的解析式; ,解关于
,解关于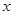 的不等式
的不等式
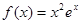 的导函数
的导函数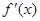 ,则不等式
,则不等式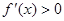 的解集为 。
的解集为 。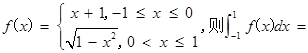 ( )
( )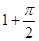
 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为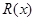 万元,且
万元,且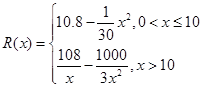 .
.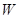 (万元)关于年产量
(万元)关于年产量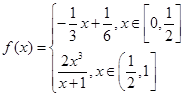 ,函数
,函数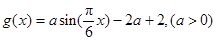 ,若存在
,若存在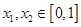 ,使得
,使得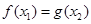 成立,则实数
成立,则实数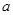 的取值范围是 。
的取值范围是 。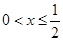 时,
时,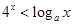 ,则
,则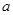 的取值范围 .
的取值范围 .