题目内容
已知f(x)是奇函数,满足f(x+2)=f(x),当x∈[0,1]时,f(x)=2x-1,则f(2)=______,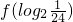 的值是 ______.
的值是 ______.
解:令x=0,f(0+2)=f(0)=20-1=0
即f(2)=0.
又当x∈[0,1],f(x+2)=f(x)=2x-1,
设t=x+2,
则有x=t-2,代入原函数
f(t)=2t-2-1
即当x∈[2,3],f(x)=2x-2-1
又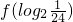 =-f(log224)=-f(2+log26)=-f(log26)=-(2log26-2-1)=-
=-f(log224)=-f(2+log26)=-f(log26)=-(2log26-2-1)=-
故答案为:0,-
分析:可先令x=0代入f(x+2)=f(x),求出f(2)的值;然后求在[2,3],函数的解析式求出答案.
点评:本题主要考查了函数的奇偶性的运用.做题时应充分利用好f(x+2)=f(x)关系式.
即f(2)=0.
又当x∈[0,1],f(x+2)=f(x)=2x-1,
设t=x+2,
则有x=t-2,代入原函数
f(t)=2t-2-1
即当x∈[2,3],f(x)=2x-2-1
又
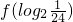 =-f(log224)=-f(2+log26)=-f(log26)=-(2log26-2-1)=-
=-f(log224)=-f(2+log26)=-f(log26)=-(2log26-2-1)=-
故答案为:0,-

分析:可先令x=0代入f(x+2)=f(x),求出f(2)的值;然后求在[2,3],函数的解析式求出答案.
点评:本题主要考查了函数的奇偶性的运用.做题时应充分利用好f(x+2)=f(x)关系式.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目