题目内容
（2011•南汇区二模）设{an}为等差数列，若a1+a5+a9=π，则tan（a2+a8）的值为
-
| 3 |
-
．| 3 |
分析：由等差数列的性质可得：a5=
，进而得到a2+a8=2a5=
，再根据特殊角的三角函数值即可得到答案．
| π |
| 3 |
| 2π |
| 3 |
解答：解：在等差数列{an}中，当m+n=p+q（m，n，p，q∈N+）时，am+an=ap+aq．
因为{an}为等差数列，且a1+a5+a9=π，
所以有a5=
，
所以a2+a8=2a5=
，
所以tan（a2+a8）=tan
=-
故答案为：-
．
因为{an}为等差数列，且a1+a5+a9=π，
所以有a5=
| π |
| 3 |
所以a2+a8=2a5=
| 2π |
| 3 |
所以tan（a2+a8）=tan
| 2π |
| 3 |
| 3 |
故答案为：-
| 3 |
点评：本题主要考查等差数列的性质，即在等差数列{an}中，当m+n=p+q（m，n，p，q∈N+）时，am+an=ap+aq，此题属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
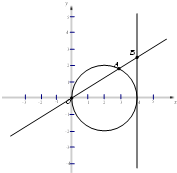（2011•南汇区二模）已知动直线y=kx交圆（x-2）2+y2=4于坐标原点O和点A，交直线x=4于点B，若动点M满足