题目内容
(本小题满分14分)
已知函数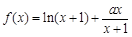
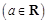 .
.
(Ⅰ)当 时,求函数
时,求函数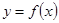 的图象在
的图象在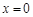 处的切线方程;
处的切线方程;
(Ⅱ)判断函数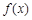 的单调性;
的单调性;
(Ⅲ)若函数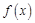 在
在 上为增函数,求
上为增函数,求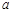 的取值范围.
的取值范围.
(Ⅰ) .
.
(Ⅱ)当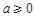 时,函数
时,函数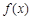 在
在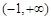 单调递增;
单调递增;
当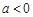 时,函数
时,函数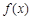 在
在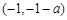 单调递减,在
单调递减,在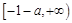 上单调递增.
上单调递增.
(Ⅲ)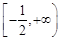 .
.
【解析】(I)当a=2时,先求出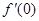 的值,即切线的斜率,然后写出点斜式方程,再化成一般式即可.
的值,即切线的斜率,然后写出点斜式方程,再化成一般式即可.
(II)先求导,可得 ,然后再对
,然后再对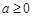 和a<0两种情况进行讨论研究其单调性.
和a<0两种情况进行讨论研究其单调性.
(III)本小题转化为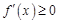 在
在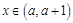 上恒成立,也可考虑求出f(x)的增区间D,然后根据
上恒成立,也可考虑求出f(x)的增区间D,然后根据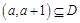 求解也可.
求解也可.
(Ⅰ)当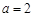 时,
时,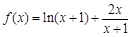 (
(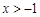 ),········································· 1分
),········································· 1分
∴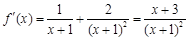 ,···································································· 2分
,···································································· 2分
∴ 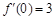 ,所以所求的切线的斜率为3.······················································· 3分
,所以所求的切线的斜率为3.······················································· 3分
又∵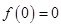 ,所以切点为
,所以切点为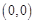 .
.
故所求的切线方程为: .······································································· 4分
.······································································· 4分
(Ⅱ)∵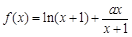 ,
,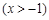
∴ ······························································· 5分
······························································· 5分
①当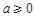 时,∵
时,∵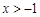 ,∴
,∴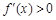 ;····························································· 6分
;····························································· 6分
②当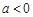 时,
时,
由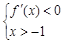 ,得
,得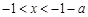 ;由
;由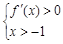 ,得
,得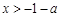 ;·························· 8分
;·························· 8分
综上,当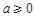 时,函数
时,函数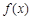 在
在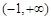 单调递增;
单调递增;
当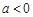 时,函数
时,函数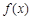 在
在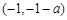 单调递减,在
单调递减,在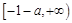 上单调递增.········ 9分
上单调递增.········ 9分
(Ⅲ)①当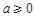 时,由(Ⅱ)可知,函数
时,由(Ⅱ)可知,函数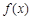 在
在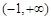 单调递增.此时,
单调递增.此时,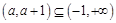 ,故
,故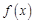 在
在 上为增函数.······································································································· 11分
上为增函数.······································································································· 11分
②当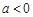 时,由(Ⅱ)可知,函数
时,由(Ⅱ)可知,函数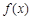 在
在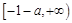 上单调递增.
上单调递增.
∵ 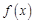 在
在 上为增函数,
上为增函数,
∴ 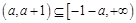 ,故
,故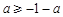 ,解得
,解得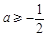 ,
,
∴ 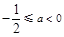 .······························································································ 13分
.······························································································ 13分
综上所述,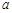 的取值范围为
的取值范围为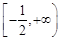 . 14分
. 14分

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)