题目内容
已知 ,符号
,符号 表示不超过
表示不超过 的最大整数,若关于
的最大整数,若关于 的方程
的方程 (
( 为常数)有且仅有3个不等的实根,则
为常数)有且仅有3个不等的实根,则 的取值范围是( ).
的取值范围是( ).
A. | B. |
C. | D. |
B
解析试题分析:因为 ,所以
,所以 ;
;
分 和
和 的情况讨论,显然有
的情况讨论,显然有 .
.
若 ,此时
,此时 ;
;
若 ,则
,则 ;
;
若 ,因为
,因为 ,故
,故 ,即
,即 .
.
且 随着
随着 的增大而增大。
的增大而增大。
若 ,此时
,此时 ;
;
若 ,则
,则 ;
;
若 ,因为
,因为 ;
; ,故
,故 ,即
,即 ,
,
且 随着
随着 的减小而增大。
的减小而增大。
又因为 一定是整数,不同的
一定是整数,不同的 对应不同的
对应不同的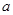 值。
值。
所以为使方程 有且仅有3个零点,只能使
有且仅有3个零点,只能使 ;或
;或








综上所述, 故选B.
故选B.
考点:本题主要考查取整函数的概念,分类讨论思想,函数的单调性.

练习册系列答案
相关题目
某家具的标价为132元,若降价以九折出售(即优惠10%),仍可获利10%(相对进货价),则该家具的进货价是( )
| A.118元 | B. 105元 | C. 106元 | D. 108元 |
已知函数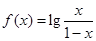 ,若
,若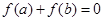 且
且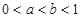 ,则
,则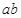 的取值范围是( )
的取值范围是( )
A.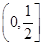 | B.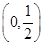 | C.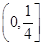 | D.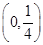 |
设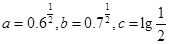 ,则
,则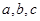 之间的关系是 ( )
之间的关系是 ( )
A.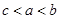 | B.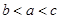 | C.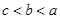 | D.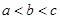 |
方程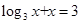 的解所在的区间为
的解所在的区间为
A.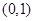 | B.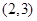 | C.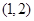 | D.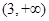 |
设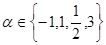 ,则使函数
,则使函数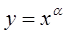 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有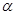 的值为( )
的值为( )
| A.-1,3 | B.-1,1 | C.1,3 | D.-1,1,3 |
已知关于 的方程
的方程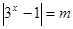 有一解,则
有一解,则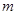 的取值范围为( )
的取值范围为( )
A.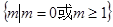 | B.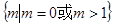 | C.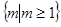 | D.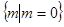 |
 是定义域R上的减函数,则函数
是定义域R上的减函数,则函数 的图象是( )
的图象是( )
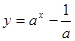
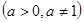 的图象可能是( )
的图象可能是( )