题目内容
如果函数f(x)=ax2+2x-3在区间(-∞,4)上是单调递增的,则实数a的取值范围是( )
A、a>-
| ||
B、a≥-
| ||
C、-
| ||
D、-
|
分析:由于a值不确定,此题要讨论,当a=0时,函数为一次函数,当a≠o时,函数为二次函数,此时分两种情况,当a>0时,函数开口向上,先减后增,当a<0时,函数开口向下,先增后减.
解答:解:(1)当a=0时,函数为一次函数f(x)=2x-3为递增函数,
(2)当a>0时,二次函数开口向上,先减后增,在区间(-∞,4)上不可能是单调递增的,故不符合;
(3)当a<0时,函数开口向下,先增后减,函数对称轴-
≥4,
解得a≥-
,又a<0,故-
≤a<0.
综合得-
≤a≤0,
故选D.
(2)当a>0时,二次函数开口向上,先减后增,在区间(-∞,4)上不可能是单调递增的,故不符合;
(3)当a<0时,函数开口向下,先增后减,函数对称轴-
| 1 |
| a |
解得a≥-
| 1 |
| 4 |
| 1 |
| 4 |
综合得-
| 1 |
| 4 |
故选D.
点评:此题主要考查函数单调性和对称轴的求解,考查二次函数的性质等基础知识,考查运算求解能力,考查数形结合思想、分类讨论思想.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
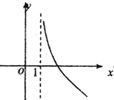
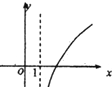
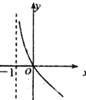

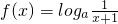 的图象大致是
的图象大致是



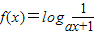 的图象大致是( )
的图象大致是( )



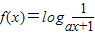 的图象大致是( )
的图象大致是( )



 的图象大致是( )
的图象大致是( )