题目内容
 如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点Cn,Dn在函数f(x)=x+
如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点Cn,Dn在函数f(x)=x+| 1 |
| x |
| A、208 | B、216 |
| C、212 | D、220 |
分析:依题意,可求得Cn(n,n+
),Dn(
,n+
)从而可求得an=4n;继而可求得a2+a3+…+a10的值.
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
解答:解:∵点Bn的坐标(n,0)(n≥2,n∈N+),顶点Cn,Dn在函数f(x)=x+
(x>0)的图象上,
∴Cn(n,n+
);
依题意知,Dn(
,n+
);
∴|AnBn|=n-
(n≥2,n∈N+),
∴an=2(n-
)+2(n-
)=4n.
∴an+1-an=4,又a1=4,
∴数列{an}是首项为4,公差为4的等差数列,
∴a2+a3+…+a10
=
=
=216.
故选:B.
| 1 |
| x |
∴Cn(n,n+
| 1 |
| n |
依题意知,Dn(
| 1 |
| n |
| 1 |
| n |
∴|AnBn|=n-
| 1 |
| n |
∴an=2(n-
| 1 |
| n |
| 1 |
| n |
∴an+1-an=4,又a1=4,
∴数列{an}是首项为4,公差为4的等差数列,
∴a2+a3+…+a10
=
| (a2+a10)×9 |
| 2 |
=
| (8+40)×9 |
| 2 |
=216.
故选:B.
点评:本题考查数列的求和,求得an=4n是关键,考查分析推理与运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
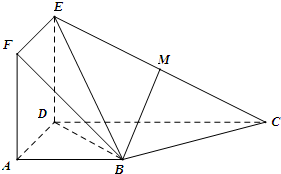 如图,矩形 ADEF与梯形ABCD 所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
如图,矩形 ADEF与梯形ABCD 所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点. 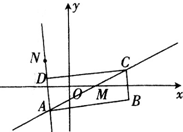 如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点N(-2,2)在AD边所在直线上,求直线AC的方程.
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点N(-2,2)在AD边所在直线上,求直线AC的方程. 如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.  (2012•德州一模)如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=1,CD=2,DE=3,M为CE的中点.
(2012•德州一模)如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=1,CD=2,DE=3,M为CE的中点. (2012•闵行区一模)如图,矩形OABC中,AB=1,OA=2,以BC中点E为圆心、以1为半径在矩形内部作四分之一圆弧CD(其中D为OA中点),点P是弧CD上一动点,PM⊥BC,垂足为M,PN⊥AB,垂足为N,则四边形PMBN的周长的最大值为
(2012•闵行区一模)如图,矩形OABC中,AB=1,OA=2,以BC中点E为圆心、以1为半径在矩形内部作四分之一圆弧CD(其中D为OA中点),点P是弧CD上一动点,PM⊥BC,垂足为M,PN⊥AB,垂足为N,则四边形PMBN的周长的最大值为