题目内容
(本题14分)设函数![]() 与
与![]() 的图像分别交直线
的图像分别交直线![]() 于点
于点![]() ,且曲线
,且曲线![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() 在点
在点![]() 处的切线平行.
处的切线平行.
(1)求函数![]() ,
,![]() 的表达式;
的表达式;
(2)设函数![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
(1)由![]() 得
得![]() ,由
,由![]() 得
得![]() .又由题意可得
.又由题意可得![]() ,即
,即![]() ,故
,故![]() ,所以
,所以![]() ,
,![]() 。——————4分
。——————4分
(2)由![]() 得
得![]() .由
.由![]() 可知
可知![]() .故当
.故当![]() 时
时![]() ,
,![]() 递减,当
递减,当![]() 时
时![]() ,
,
![]() 递增,所以函数
递增,所以函数![]() 的最小值为
的最小值为![]() .———9分
.———9分
(3)当![]() 时,
时,![]() ,而
,而![]() ,故:
,故:
当![]() 时,不等式
时,不等式![]() 在
在![]() 均成立.
均成立.
当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,故要使
,故要使![]() 恒成立,则必需
恒成立,则必需![]() ,即
,即![]() .事实上,当
.事实上,当![]() 时,
时,![]() .故可知此时
.故可知此时![]() .
.
综上可知当![]() 时,不等式
时,不等式![]() 在
在![]() 均成立.————14分.
均成立.————14分.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
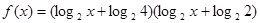 的定义域为
的定义域为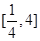 ,
,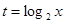 ,求
,求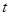 的取值范围;
的取值范围;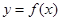 的最大值与最小值,并求出最值时对应的
的最大值与最小值,并求出最值时对应的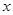 的值.
的值.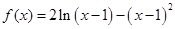 .
.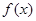 的单调递增区间;
的单调递增区间;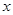 的方程
的方程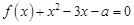 在区间
在区间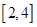 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数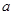 的取值范围.
的取值范围.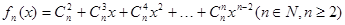 ,当
,当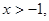 且
且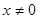 时,证明:
时,证明: 恒成立
恒成立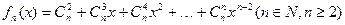 ,当
,当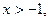 且
且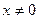 时,证明:
时,证明: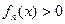 恒成立
恒成立