Question

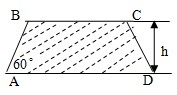（2008•杨浦区二模）建造一条防洪堤，其断面为等腰梯形，腰与底边成角为60°（如图），考虑到防洪堤坚固性及石块用料等因素，设计其断面面积为6

3

平   方米，为了使堤的上面与两侧面的水泥用料最省，则断面的外周长（梯形的上底线段BC与两腰长的和）要最小．
求外周长的最小值，此时防洪堤高h为多少米？

Answer 1

分析：本题是一个应用题，研究的是用料最省，此类题一般要建立函数关系，利用求最值得出最佳方案，由题设条件，此断面的面积已知，求外周长的最小值，引入变量防洪堤高h建立外周长关于h的函数，再根据函数的形式求最值即可

解答：解：由题意，如图AD=BC+2×hcot60°=BC+

2 3

3

h，------------------------------------------------------（2分）
所以6

3

=

1

2

(AD+BC)h=

1

2

(2BC+

2 3

3

h)h，---------------------------------------------（3分）
得BC=

6 3

h

-

3

3

h．-----------------------------------------------------------------------------（4分）
设外周长为l，则l=2AB+BC=

2h

sin60°

+

6 3

h

-

3

3

h，-----------------------------（7分）
=

3

h+

6 3

h

≥6

2

；----------------------------------------------------------------------------（10分）
当

3

h=

6 3

h

，即h=

6

时等号成立．----------------------------------------------------（12分）
外周长的最小值为6

2

米，此时堤高h为

6

米．-----------------------------------------（14分）

点评：本题考查已知三角函数模型的应用问题，解题的关键是建立起符合条件的函数的模型，由于本题是一个研究用料最省的问题，故建立函数模型后要根据函数的形式选择求最值的方法，由于本题在建立函数模型中出现了积为定值的形式，故采取了用基本不等式求最值，利用此法求最值有一易错点，即忘记验证等号成立的条件，对规律性强的题一定要把握好规律，准确记忆