题目内容
已知数列的首项为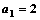 ,前
,前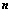 项和为
项和为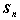 ,且对任意的
,且对任意的 ,当
,当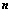 ≥2时,
≥2时,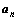 总是
总是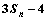 与
与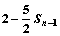 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设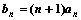 ,
,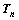 是数列
是数列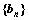 的前
的前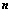 项和,
项和, ,求
,求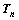 ;
;
(Ⅲ)设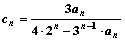 ,
,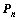 是数列
是数列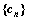 的前项和,
的前项和, ,试证明:
,试证明: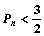 .
.
【答案】
(Ⅰ)解: 当

又

 …………4分
…………4分
(Ⅱ)解:由(Ⅰ),知
则
 …………①
…………①
 …………② …………5分
…………② …………5分
①-②,得



 …………8分
…………8分
(Ⅲ)证明:
 ……………12分
……………12分

 …………14分
…………14分

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
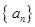 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称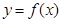 使得
使得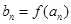 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称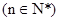 .
.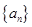 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若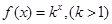 是数列
是数列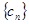 的首项为2010,
的首项为2010,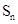 是数列
是数列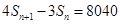 ,证明
,证明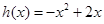 ,
,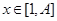 ,和数列1,
,和数列1,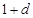 ,
,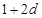 ,(
,(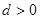 )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.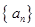 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称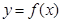 使得
使得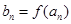 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称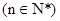 .
.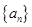 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若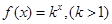 是数列
是数列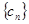 的首项为2010,
的首项为2010,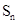 是数列
是数列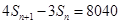 ,证明
,证明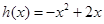 ,
,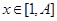 ,和数列1,
,和数列1,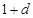 ,
,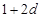 ,(
,(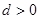 )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由. 的首项为
的首项为 =3,通项
=3,通项 与前n项和
与前n项和 之间满足2
之间满足2 是等差数列,并求公差;
是等差数列,并求公差;