题目内容
设关于x的函数f(x)=mx2-(2m2+4m+1)x+(m+2)lnx,其中m为R上的常数,若函数f(x)在x=1处取得极大值0.
(1)求实数m的值;
(2)若函数f(x)的图像与直线y=k有两个交点,求实数k的取值范围;
(3)设函数![]() ,若对任意的x∈[1,2],2f(x)≥g(x)+4x-2x2恒成立,求实数p的取值范围.
,若对任意的x∈[1,2],2f(x)≥g(x)+4x-2x2恒成立,求实数p的取值范围.
答案:
解析:
解析:
解:(1)![]()
![]()
因为函数![]() 在
在![]() 处取得极大值
处取得极大值![]()
所以, 解
解![]()
(2)由(Ⅰ)知![]() ,令
,令![]() 得
得![]() 或
或![]() (舍去)
(舍去)
在![]() 上函数
上函数![]() 单调递增,在
单调递增,在![]() 上函数
上函数![]() 单调递减
单调递减
当![]() 时,
时,![]() ,所以,函数
,所以,函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,所以,当
上单调递减,所以,当![]() 时,函数
时,函数![]() 取得最大值,
取得最大值,![]()
当![]() 时,
时,![]() 即
即![]()
所以,当![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 有两个交点,
有两个交点,


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
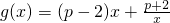 ,其中p≤0,若对任意的x∈[1,2],总有2f(x)≥g(x)+4x-2x2成立,求p的取值范围.
,其中p≤0,若对任意的x∈[1,2],总有2f(x)≥g(x)+4x-2x2成立,求p的取值范围. ,其中p≤0,若对任意的x∈[1,2],总有2f(x)≥g(x)+4x-2x2成立,求p的取值范围.
,其中p≤0,若对任意的x∈[1,2],总有2f(x)≥g(x)+4x-2x2成立,求p的取值范围. ,其中p≤0,若对任意的x∈[1,2],总有2f(x)≥g(x)+4x-2x2成立,求p的取值范围.
,其中p≤0,若对任意的x∈[1,2],总有2f(x)≥g(x)+4x-2x2成立,求p的取值范围. 时,求a的值,并求此时f(x)的最大值。(12分)
时,求a的值,并求此时f(x)的最大值。(12分)