题目内容
已知函数f(x)=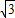 sin(π-x)+cosx
sin(π-x)+cosx(1)求f(
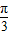 );
);(2)求f(x)的值域;
(3)将函数y=f(x)的图象上各点的横坐标缩短到原来的
 ,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)的单调增区间.
,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)的单调增区间.
【答案】分析:(1)将x= 代入函数解析式,计算即可得到结果;
代入函数解析式,计算即可得到结果;
(2)f(x)解析式利用诱导公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域即可求出f(x)的值域;
(3)根据题意及f(x)解析式求出g(x)解析式,根据正弦函数的递增区间求出x的范围,即可确定出g(x)的递增区间.
解答:解:(1)根据题意得:f( )=
)= sin(π-
sin(π- )+cos
)+cos =
= ×
× +
+ =2;
=2;
(2)f(x)= sin(π-x)+cosx=
sin(π-x)+cosx= sinx+cosx=2sin(x+
sinx+cosx=2sin(x+ ),
),
∵-1≤2sin(x+ )≤1,
)≤1,
∴f(x)的值域为[-2,2];
(3)由(2)知,f(x)=2sin(x+ ),
),
依题意知g(x)=2sin(2x+ ),
),
令2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈Z,得kπ-
,k∈Z,得kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z,
则函数y=g(x)的单调增区间是[kπ- ,kπ+
,kπ+ ],k∈Z.
],k∈Z.
点评:此题考查了两角和与差的正弦函数公式,诱导公式,正弦函数的定义域与值域,以及正弦函数的递增区间,熟练掌握公式是解本题的关键.
 代入函数解析式,计算即可得到结果;
代入函数解析式,计算即可得到结果;(2)f(x)解析式利用诱导公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域即可求出f(x)的值域;
(3)根据题意及f(x)解析式求出g(x)解析式,根据正弦函数的递增区间求出x的范围,即可确定出g(x)的递增区间.
解答:解:(1)根据题意得:f(
 )=
)= sin(π-
sin(π- )+cos
)+cos =
= ×
× +
+ =2;
=2;(2)f(x)=
 sin(π-x)+cosx=
sin(π-x)+cosx= sinx+cosx=2sin(x+
sinx+cosx=2sin(x+ ),
),∵-1≤2sin(x+
 )≤1,
)≤1,∴f(x)的值域为[-2,2];
(3)由(2)知,f(x)=2sin(x+
 ),
),依题意知g(x)=2sin(2x+
 ),
),令2kπ-
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈Z,得kπ-
,k∈Z,得kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z,则函数y=g(x)的单调增区间是[kπ-
 ,kπ+
,kπ+ ],k∈Z.
],k∈Z.点评:此题考查了两角和与差的正弦函数公式,诱导公式,正弦函数的定义域与值域,以及正弦函数的递增区间,熟练掌握公式是解本题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
