Question

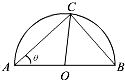某风景区在一个直径AB为100米的半圆形花园中设计一条观光线路（如图所示）．在点A与圆弧上的一点C之间设计为直线段小路，在路的两侧边缘种植绿化带；从点C到点B设计为沿弧的弧形小路，在路的一侧边缘种植绿化带．（注：小路及绿化带的宽度忽略不计）
（1）设∠BAC=θ（弧度），将绿化带总长度表示为θ的函数S（θ）；
（2）试确定θ的值，使得绿化带总长度最大．

Answer 1

分析：（1）利用三角函数结合弧长公式，可将绿化带总长度表示为θ的函数S（θ）；
（2）求导数，确定函数的单调性，即可确定θ的值，使得绿化带总长度最大．

解答：解：（1）由题意，AC=100cosθ，直径AB为100米，
∴半径为50米，圆心角为2θ，∴

BC

=100θ，
∴绿化带总长度S（θ）=200cosθ+100θ（θ∈（0，

π

2

）；
（2）∵S（θ）=200cosθ+100θ，
∴S′（θ）=-200sinθ+100，
令S′（θ）=0，可得θ=

π

6

．
函数在（0，

π

6

）上单调递增，在（

π

6

，

π

2

）上单调递减，
∴θ=

π

6

时，绿化带总长度最大．

点评：利用导数可以解决实际问题中的最值问题，关键是确定函数解析式，正确运用导数工具，确定函数的单调性．