题目内容
在直角坐标系O—xyz中,(1)求![]() 与
与![]() 的夹角α的大小;
的夹角α的大小;
(2)设n=(1,p,q),且n⊥平面SBC,求n;
(3)求OA与平面SBC的夹角;
(4)求点O到平面SBC的距离;
(5)求异面直线SC与OB间的距离.
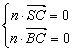
解:(1)如图,![]() =
=![]() -
- ![]() =(2,0,-1),
=(2,0,-1), ![]() =
=![]() +
+![]() =(1,1,0),则
=(1,1,0),则
|![]() |=
|=![]() =
=![]() ,|OB|=
,|OB|=![]() =
=![]() .
.
cosα=cos〈![]() ,
,![]() 〉=
〉=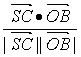 =
=![]() =
=![]() ,α=arccos
,α=arccos![]() .
.
(2)∵n⊥平面SBC,
∴n⊥![]() 且n⊥
且n⊥![]() ,即
,即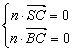
∵![]() =(2,0,-1),
=(2,0,-1), ![]() =
=![]() -
-![]() =(1,-1,0),
=(1,-1,0),
∴![]() ∴
∴![]() 即n=(1,1,2).
即n=(1,1,2).
(3)OA与平面SBC所成的角θ和OA与平面SBC的法线所夹角互余,故可先求![]() 与n所成的角.
与n所成的角.
![]() =(0,1,0),|
=(0,1,0),| ![]() |=1,|n|=
|=1,|n|=![]() =
=![]() .
.
∴cos〈![]() ,n〉=
,n〉= =
=![]() =
=![]() ,
,
即〈![]() ,n〉=arccos
,n〉=arccos![]() .
.
∴θ=![]() -arccos
-arccos![]() .
.
(4)点O到平面SBC的距离即为![]() 在n上的投影的绝对值,
在n上的投影的绝对值,
∴d=|![]() ·
·![]() |=
|=![]() =
=![]() .
.
(5) ![]() 在异面直线SC、OB的公垂线方向上的投影的绝对值即为两条异面直线间的距离,故先求与SC、OB均垂直的向量m.
在异面直线SC、OB的公垂线方向上的投影的绝对值即为两条异面直线间的距离,故先求与SC、OB均垂直的向量m.
设m=(x,y,1),m⊥![]() 且m⊥
且m⊥![]() ,
,
则m·![]() =0,且m·
=0,且m·![]() =0.
=0.
∴![]() 即
即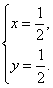
∴m=(![]() ,-
,-![]() ,1),d′=|
,1),d′=|![]() ·
·![]() |=
|=![]()
=![]() .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.