题目内容
已知集合P={(x,y)|2x+y-2=0},Q={(x,y)|2x2-ay2+(2a-1)xy+4ay-2=0},若P?Q,则实数a的值为( )
分析:对选项一一验证:当a=
时,2x2-ay2+(2a-1)xy+4ay-2=0变为:2x2-y2+2y-2=0,因式分解得:(2x+y-2)(x-
y+1)=0故集合Q表示两条相交直线,其中之一是集合P={(x,y)|2x+y-2=0}表示的直线,从而得出正确选项.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:对选项一一验证:
当a=
时,2x2-ay2+(2a-1)xy+4ay-2=0变为:
2x2-y2+2y-2=0,因式分解得:
(2x+y-2)(x-
y+1)=0,⇒2x+y-2=0或x-
y+1=0,
故集合Q表示两条相交直线2x+y-2=0或x-
y+1=0,
其中之一是集合P={(x,y)|2x+y-2=0}表示的直线,
故P?Q,
故选B.
当a=
| 1 |
| 2 |
2x2-y2+2y-2=0,因式分解得:
(2x+y-2)(x-
| 1 |
| 2 |
| 1 |
| 2 |
故集合Q表示两条相交直线2x+y-2=0或x-
| 1 |
| 2 |
其中之一是集合P={(x,y)|2x+y-2=0}表示的直线,
故P?Q,
故选B.
点评:本小题主要考查集合关系中的参数取值问题、直线的方程、二次项的因式分解等基础知识,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
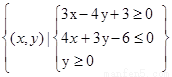 ,Q={(x,y)|(x-a)2+(y-b)2≤r2(r>0), 若“点M∈P”是“点M∈Q”的必要条件,则当r最大时ab的值是_____
,Q={(x,y)|(x-a)2+(y-b)2≤r2(r>0), 若“点M∈P”是“点M∈Q”的必要条件,则当r最大时ab的值是_____