题目内容
已知数列{an}的前n项和Sn满足2Sn-3an+2n=0(其中n∈N*).
(Ⅰ)求证:数列{an+1}是等比数列,并求数列{an}的通项公式;
(Ⅱ)若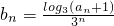 ,且Tn=b1+b2+…+bn,求Tn;
,且Tn=b1+b2+…+bn,求Tn;
(Ⅲ)设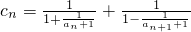 ,数列{cn}的前n项和为Mn,求证:
,数列{cn}的前n项和为Mn,求证: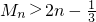 .
.
(Ⅰ)证明:∵2Sn-3an+2n=0①,
∴2Sn+1-3an+1+2(n+1)②,
②-①得:2an+1-3(an+1-an)+2=0,
∴an+1=3an+3.
∴an+1+1=3(an+1),
∴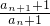 =3,
=3,
又2a1-3a1+2=0,故a1=2,a1+1=3,
∴数列{an+1}是首项为3,公比为3的等比数列,
∴an+1=3•3n-1=3n,
∴an=3n-1.
(Ⅱ)∵bn=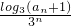 =
=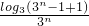 =
=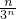 ,
,
∴Tn=b1+b2+…+bn= +
+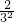 +
+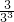 +…+
+…+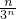 ,③
,③
 Tn=
Tn= +
+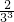 +…+
+…+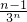 +
+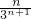 ④
④
③-④得: Tn=
Tn= +
+ +…+
+…+ -
-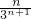 =
=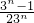 -
-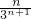 ,
,
∴Tn= -
- •
• .
.
(Ⅲ)∵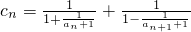
=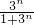 +
+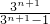
=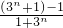 +
+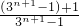
=2- +
+ .
.
∴Mn=c1+c2+…+cn=2n-[(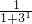 -
- )+(
)+(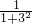 -
-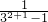 )+…+(
)+…+( -
- )].
)].
∵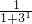 <
< ,
, >
>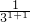 ,-
,- <-
<-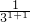 ,
,
∴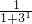 -
- <
< -
-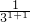 ,⑤
,⑤
同理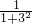 -
-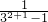 <
<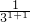 -
-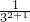 ,⑥
,⑥
…
 -
- <
< -
-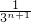 ⑦
⑦
∴(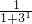 -
- )+(
)+(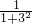 -
-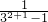 )+…+(
)+…+( -
- )<
)< -
-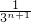 <
<
∴-[(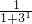 -
- )+(
)+(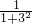 -
-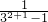 )+…+(
)+…+( -
- )]>-
)]>-
∴Mn>2n- .
.
分析:(Ⅰ)由2Sn-3an+2n=0①,可得2Sn+1-3an+1+2(n+1)②,由①②即可证得数列{an+1}是等比数列,并求数列{an}的通项公式;
(Ⅱ)求得bn=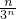 ,利用错位相减法即可求得Tn;
,利用错位相减法即可求得Tn;
(Ⅲ)可求得cn═2- +
+ ,Mn=c1+c2+…+cn=2n-[(
,Mn=c1+c2+…+cn=2n-[(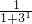 -
- )+(
)+(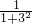 -
-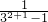 )+…+(
)+…+( -
- )].利用放缩法与累加法即可证明结论.
)].利用放缩法与累加法即可证明结论.
点评:本题考查数列与不等式的综合,着重考查等比关系的确定于数列的求和,突出错位相减法与放缩法、累加法的应用,综合题性强,属于难题.
∴2Sn+1-3an+1+2(n+1)②,
②-①得:2an+1-3(an+1-an)+2=0,
∴an+1=3an+3.
∴an+1+1=3(an+1),
∴
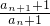 =3,
=3,又2a1-3a1+2=0,故a1=2,a1+1=3,
∴数列{an+1}是首项为3,公比为3的等比数列,
∴an+1=3•3n-1=3n,
∴an=3n-1.
(Ⅱ)∵bn=
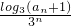 =
=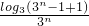 =
=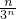 ,
,∴Tn=b1+b2+…+bn=
 +
+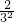 +
+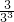 +…+
+…+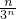 ,③
,③ Tn=
Tn= +
+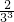 +…+
+…+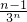 +
+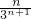 ④
④③-④得:
 Tn=
Tn= +
+ +…+
+…+ -
-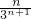 =
=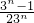 -
-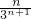 ,
,∴Tn=
 -
- •
• .
.(Ⅲ)∵
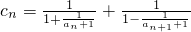
=
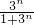 +
+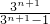
=
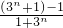 +
+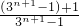
=2-
 +
+ .
.∴Mn=c1+c2+…+cn=2n-[(
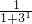 -
- )+(
)+(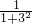 -
-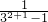 )+…+(
)+…+( -
- )].
)].∵
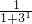 <
< ,
, >
>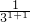 ,-
,- <-
<-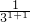 ,
,∴
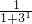 -
- <
< -
-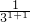 ,⑤
,⑤同理
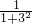 -
-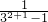 <
<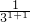 -
-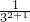 ,⑥
,⑥…
 -
- <
< -
-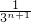 ⑦
⑦∴(
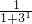 -
- )+(
)+(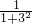 -
-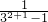 )+…+(
)+…+( -
- )<
)< -
-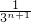 <
<
∴-[(
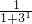 -
- )+(
)+(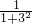 -
-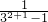 )+…+(
)+…+( -
- )]>-
)]>-
∴Mn>2n-
 .
.分析:(Ⅰ)由2Sn-3an+2n=0①,可得2Sn+1-3an+1+2(n+1)②,由①②即可证得数列{an+1}是等比数列,并求数列{an}的通项公式;
(Ⅱ)求得bn=
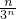 ,利用错位相减法即可求得Tn;
,利用错位相减法即可求得Tn;(Ⅲ)可求得cn═2-
 +
+ ,Mn=c1+c2+…+cn=2n-[(
,Mn=c1+c2+…+cn=2n-[(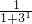 -
- )+(
)+(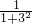 -
-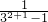 )+…+(
)+…+( -
- )].利用放缩法与累加法即可证明结论.
)].利用放缩法与累加法即可证明结论.点评:本题考查数列与不等式的综合,着重考查等比关系的确定于数列的求和,突出错位相减法与放缩法、累加法的应用,综合题性强,属于难题.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |