题目内容
抛物线y=g(x)过点O(0,0)、A(m,0)与点P(m+1,m+1),其中m>n>0,b<a,设函数f(x)=(x-n)g(x)在x=a和x=b处取到极值.(1)用m,x表示y=g(x)并比较a,b,m,n的大小(要求按从小到大排列);
(2)若
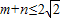 ,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).
,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).
【答案】分析:(1)设抛物线方程,利用抛物线过点P,可得k=1,从而可得y=g(x)=x(x-m),利用函数f(x)在x=a和x=b处取到极值,结合m>n>0,即可比较a,b,m,n的大小;
(2)设切点Q(x,y),求导数,可得切线的方程,利用切线过原点,得两条两条切线的斜率,根据 ,两条切线垂直,即可求得函数解析式.
,两条切线垂直,即可求得函数解析式.
解答:解:(1)由抛物线经过点O(0,0)、A(m,0)
设抛物线方程y=kx(x-m)(k≠0),
又抛物线过点P(m+1,m+1),则m+1=k(m+1)(m+1-m),得k=1,
所以y=g(x)=x(x-m). …(3分)
∴f(x)=(x-n)g(x)=x3-(m+n)x2+mnx,
∴f′(x)=3x2-2(m+n)x+mn,
∵函数f(x)在x=a和x=b处取到极值,…(5分)
∴f′(a)=0,f′(b)=0,
∵m>n>0,
∴f′(m)=3m2-2(m+n)m+mn=m(m-n)>0 …(7分)
f′(n)=3n2-2(m+n)n+mn=n(n-m)<0,
又b<a,故b<n<a<m. …(8分)
(2)设切点Q(x,y),则切线的斜率k=f′(x)=3x2-2(m+n)x+mn
又y= -(m+n)
-(m+n) +mnx,所以切线的方程是y-
+mnx,所以切线的方程是y- +(m+n)
+(m+n) -mnx=[3x2-2(m+n)x+mn](x-x)…(9分)
-mnx=[3x2-2(m+n)x+mn](x-x)…(9分)
又切线过原点,故- +(m+n)
+(m+n) -mnx=[3x2-2(m+n)x+mn](-x)
-mnx=[3x2-2(m+n)x+mn](-x)
所以2 -(m+n)
-(m+n) =0,解得x=0,或x=
=0,解得x=0,或x= . …(10分)
. …(10分)
两条切线的斜率为k1=f′(0)=mn, ,
,
由 ,得(m+n)2≥8,∴
,得(m+n)2≥8,∴ ,
,
∴ ,
,
所以 …(12分)
…(12分)
又两条切线垂直,故k1k2=-1,
所以上式等号成立,有 ,且mn=1.
,且mn=1.
所以f(x)=x3-(m+n)x2+mnx=x3- x2+x. …13 分
x2+x. …13 分
点评:本题考查导数知识的运用,考查导数的几何意义,考查学生分析解决问题的能力,属于中档题.
(2)设切点Q(x,y),求导数,可得切线的方程,利用切线过原点,得两条两条切线的斜率,根据
 ,两条切线垂直,即可求得函数解析式.
,两条切线垂直,即可求得函数解析式.解答:解:(1)由抛物线经过点O(0,0)、A(m,0)
设抛物线方程y=kx(x-m)(k≠0),
又抛物线过点P(m+1,m+1),则m+1=k(m+1)(m+1-m),得k=1,
所以y=g(x)=x(x-m). …(3分)
∴f(x)=(x-n)g(x)=x3-(m+n)x2+mnx,
∴f′(x)=3x2-2(m+n)x+mn,
∵函数f(x)在x=a和x=b处取到极值,…(5分)
∴f′(a)=0,f′(b)=0,
∵m>n>0,
∴f′(m)=3m2-2(m+n)m+mn=m(m-n)>0 …(7分)
f′(n)=3n2-2(m+n)n+mn=n(n-m)<0,
又b<a,故b<n<a<m. …(8分)
(2)设切点Q(x,y),则切线的斜率k=f′(x)=3x2-2(m+n)x+mn
又y=
 -(m+n)
-(m+n) +mnx,所以切线的方程是y-
+mnx,所以切线的方程是y- +(m+n)
+(m+n) -mnx=[3x2-2(m+n)x+mn](x-x)…(9分)
-mnx=[3x2-2(m+n)x+mn](x-x)…(9分)又切线过原点,故-
 +(m+n)
+(m+n) -mnx=[3x2-2(m+n)x+mn](-x)
-mnx=[3x2-2(m+n)x+mn](-x)所以2
 -(m+n)
-(m+n) =0,解得x=0,或x=
=0,解得x=0,或x= . …(10分)
. …(10分)两条切线的斜率为k1=f′(0)=mn,
 ,
,由
 ,得(m+n)2≥8,∴
,得(m+n)2≥8,∴ ,
,∴
 ,
,所以
 …(12分)
…(12分)又两条切线垂直,故k1k2=-1,
所以上式等号成立,有
 ,且mn=1.
,且mn=1.所以f(x)=x3-(m+n)x2+mnx=x3-
 x2+x. …13 分
x2+x. …13 分点评:本题考查导数知识的运用,考查导数的几何意义,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
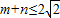 ,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).
,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).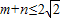 ,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).
,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).