题目内容
设函数f(x)=|3x-1|+x+2.
(1)解不等式f(x)≤3;
(2)若不等式f(x)>a的解集为![]() R,求a的取值范围.
R,求a的取值范围.
(1)方法一:当x≥![]() 时,f(x)=3x-1+x+2=4x+1≤3,
时,f(x)=3x-1+x+2=4x+1≤3,
即x≤![]() ,∴
,∴![]() ≤x≤
≤x≤![]() .
.
当x<![]() 时,
时,
f(x)=1-3x+x+2=-2x+3≤3,
即x≥0,∴0≤x<![]() .
.
综上所述,其解集为{x|0≤x≤![]() }.
}.
方法二:|3x-1|+x+2≤3.
∴|3x-1|≤1-x.
∴x-1≤3x-1≤1-x.
∴{x|0≤x≤![]() }.
}.
(2)f(x)= ,
,
当x≥![]() 时,
时,![]() f(x)单调递增;
f(x)单调递增;
当x<![]() 时,f(x)单调递减,
时,f(x)单调递减,
∴f(x)min=f(![]() )=
)=![]() .
.
要使不等式f(x)>a的解集为R,
只需f(x)min>a即可,即![]() >a.
>a.
∴a的取值范围为(-∞,![]() ).
).

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
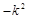 +1在区间(0,4)上是减函数,则的取值范围 (
)
A.
+1在区间(0,4)上是减函数,则的取值范围 (
)
A.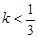 B.
B. C.
C.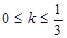 D.
D.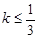
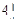 上是减函数,则实数a的范围是( )
上是减函数,则实数a的范围是( )