题目内容
若函数
的图象在x=1处的切线l过点
，且l与圆C：x2+y2=1相交，则点（a，b）与圆C的位置关系是（ ）A．点在圆内
B．点在圆外
C．点在圆上
D．不能确定
【答案】分析：函数在某点的导数就是函数在此点的切线斜率，写出切线方程，直线和圆相切时，圆心到直线的距离小于圆的半径．
解答：解：∵函数
的图象在x=1处的切线l过点
，
∴切线的斜率是f′（1）=-
，∴y+
=-
（x-0），
ax+by+1=0，∵l与圆C：x2+y2=1相交，
∴
＜1，a2+b2＞1，
∴点（a，b）与圆C的位置关系是：点在圆外．
故答案选B．
点评：本题考查利用导数求切线斜率，直线与圆、点与圆的位置关系．
解答：解：∵函数
的图象在x=1处的切线l过点，∴切线的斜率是f′（1）=-
，∴y+=-（x-0），ax+by+1=0，∵l与圆C：x2+y2=1相交，
∴
＜1，a2+b2＞1，∴点（a，b）与圆C的位置关系是：点在圆外．
故答案选B．
点评：本题考查利用导数求切线斜率，直线与圆、点与圆的位置关系．
练习册系列答案
名校课堂系列答案
相关题目
，若函数
的图象在x=1处的切线平行于x轴且数列
满足
的关系式；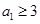
，求证：任意
，都有
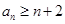成立。
的图象在x=1处的切线l过点
，且l与圆C：x2+y2=1相交，则点（a，b）与圆C的位置关系是（ ）
的图象在x=1处的切线l过点
，且l与圆C：x2+y2=1相交，则点（a，b）与圆C的位置关系是（ ）
的图象在x=1处的切线l过点
，且l与圆C：x2+y2=1相交，则点（a，b）与圆C的位置关系是（ ）