题目内容
(不等式选讲选做题)若a、b、c∈R,且a2+2b2+3c2=6,则a+b+c的最小值是______.
由柯西不等式得:
(1+
+
)×(a2+2b2+3c2)≥(a+b+c)2
×6=11≥(a+b+c)2
故-
≤a+b+c≤
故a+b+c最小值是-
故答案为:-
(1+
| 1 |
| 2 |
| 1 |
| 3 |
| 11 |
| 6 |
故-
| 11 |
| 11 |
故a+b+c最小值是-
| 11 |
故答案为:-
| 11 |

练习册系列答案
相关题目
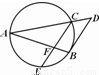
 ,则线段CD的长为 .
,则线段CD的长为 .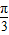 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .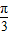 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .