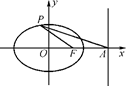
题目内容
已知椭圆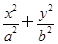
＝1(a＞b＞c＞0，a2＝b2＋c2)的左、右焦点分别为F1，F2，若以F2为圆心，b－c为半径作圆F2，过椭圆上一点P作此圆的切线，切点为T，且PT的最小值为
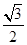(a－c)，则椭圆的离心率e的取值范围是________．
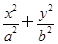＝1(a＞b＞c＞0，a2＝b2＋c2)的左、右焦点分别为F1，F2，若以F2为圆心，b－c为半径作圆F2，过椭圆上一点P作此圆的切线，切点为T，且PT的最小值为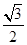(a－c)，则椭圆的离心率e的取值范围是________．
≤e＜
因为PT＝
(b＞c)，而PF2的最小值为a－c，所以PT的最小值为
.依题意有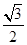，≥(a－c)，
所以(a－c)2≥4(b－c)2，所以a－c≥2(b－c)，所以a＋c≥2b，所以(a＋c)2≥4(a2－c2)，
所以5c2＋2ac－3a2≥0，所以5e2＋2e－3≥0 ①.
又b＞0，所以b2＞c2，所以a2－c2＞c2，
所以2e2＜1②，联立①②，得≤e＜.
(b＞c)，而PF2的最小值为a－c，所以PT的最小值为.依题意有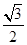，≥(a－c)，所以(a－c)2≥4(b－c)2，所以a－c≥2(b－c)，所以a＋c≥2b，所以(a＋c)2≥4(a2－c2)，
所以5c2＋2ac－3a2≥0，所以5e2＋2e－3≥0 ①.
又b＞0，所以b2＞c2，所以a2－c2＞c2，
所以2e2＜1②，联立①②，得
≤e＜.
练习册系列答案
相关题目
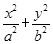＝1(a>b>0，a、b为常数)，动圆C1：x2＋y2＝
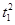，b<t1<a.点A1、A2分别为C0的左、右顶点，C1与C0相交于A、B、C、D四点．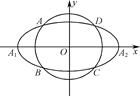
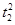与C0相交于A′，B′，C′，D′四点，其中b<t2<a，t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等，证明：
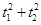为定值．
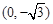)和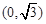
，并且经过点
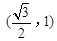，抛物线的顶点E在坐标原点，焦点恰好是椭圆C的右顶点F．
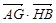的最小值．
＝1(a>b>0)的左、右顶点，椭圆长半轴的长等于焦距，且直线x＝4是它的右准线．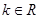
，直线
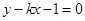与椭圆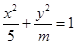
恒有公共点，则实数
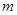的取值范围是
＝1的位置关系是________．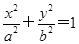
＝1(a＞b＞0)，点P
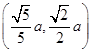在椭圆上．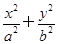
＝1(a>b>0)的右焦点F，其右准线与x轴的交点为A，在椭圆上存在点P满足线段AP的垂直平分线过点F，则椭圆离心率的取值范围是________．