题目内容
某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示．
| 用煤（吨） | 用电（千瓦） | 产值（万元） | |
| 甲产品 | 7 | 20 | 8 |
| 乙产品 | 3 | 50 | 12 |
解：设该厂每天安排生产甲产品x吨，乙产品y吨，日产值为z，可得z=8x+12y，
其中x、y满足约束条件
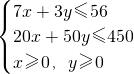
作出可行域，如右图所示
将直线l：z=8x+12y进行平移，由图可知当直线l经过可行域上的点M时，
直线在y轴上的截距最大，目标函数z同时达到最大值
解方程组
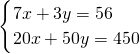，得M（5，7）∴z的最大值为zmax=8×5+12×7=124
答：该厂每天安排生产甲产品5吨，乙产品7吨，可得日产值为z的最大值为124万元．
分析：设该厂每天安排生产甲产品x吨，乙产品y吨，可得目标函数为z=8x+12y．根据题意，建立关于x、y的不等式组并作出可行域，利用直线平移的方法可得当x=5且y=7时，目标函数z的最大值为124，由此即可得到本题答案．
点评：本题给出实际问题，求该厂如何安排生产，使得该厂日产值达最大值，着重考查了二元一次不等式组表示的平面区域和简单线性规划的应用等知识，属于基础题．
练习册系列答案
相关题目