题目内容
已知函数f(x)=sin cos
cos +
+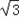 cos2
cos2 .
.
(1)求方程f(x)=0的解集;
(2)如果△ABC的三边a,b,c满足b2=ac,且边b所对的角为x,求角x的取值范围及此时函数f(x)的值域.
 cos
cos +
+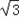 cos2
cos2 .
.(1)求方程f(x)=0的解集;
(2)如果△ABC的三边a,b,c满足b2=ac,且边b所对的角为x,求角x的取值范围及此时函数f(x)的值域.
解:(1)由f(x)=0,得
sin cos
cos +
+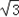 cos2
cos2 =cos
=cos (sin
(sin +
+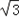 cos
cos )=0,
)=0,
由cos =0,得
=0,得 =kπ+
=kπ+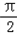 ,
,
∴x=2kπ+π(k∈Z);
由sin +
+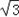 cos
cos =0,得tan
=0,得tan =﹣
=﹣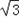 ,
,
∴ =kπ﹣
=kπ﹣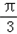 ,即x=2kπ﹣
,即x=2kπ﹣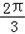 (k∈Z),
(k∈Z),
则方程f(x)=0的解集为{x|2kπ+π或2kπ﹣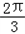 (k∈Z)};
(k∈Z)};
(2)∵b2=ac,且a2+c2≥2ac(当且仅当a=c时取等号),
∴由余弦定理得cosB=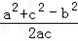 =
=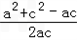 ≥
≥ ,
,
又B为三角形的内角,∴0<B≤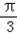 ,
,
由题意得x=B,即x∈(0,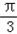 ],
],
f(x)= sinx+
sinx+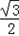 (cosx+1)=
(cosx+1)= sinx+
sinx+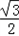 cosx+
cosx+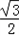 =sin(x+
=sin(x+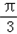 )+
)+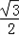 ,
,
∵x+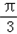 ∈(
∈(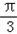 ,
,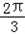 ],
],
则此时函数f(x)的值域为[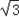 ,
,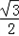 +1].
+1].
sin
 cos
cos +
+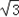 cos2
cos2 =cos
=cos (sin
(sin +
+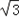 cos
cos )=0,
)=0,由cos
 =0,得
=0,得 =kπ+
=kπ+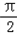 ,
,∴x=2kπ+π(k∈Z);
由sin
 +
+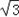 cos
cos =0,得tan
=0,得tan =﹣
=﹣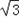 ,
,∴
 =kπ﹣
=kπ﹣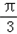 ,即x=2kπ﹣
,即x=2kπ﹣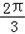 (k∈Z),
(k∈Z),则方程f(x)=0的解集为{x|2kπ+π或2kπ﹣
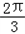 (k∈Z)};
(k∈Z)};(2)∵b2=ac,且a2+c2≥2ac(当且仅当a=c时取等号),
∴由余弦定理得cosB=
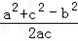 =
=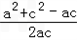 ≥
≥ ,
,又B为三角形的内角,∴0<B≤
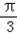 ,
,由题意得x=B,即x∈(0,
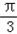 ],
],f(x)=
 sinx+
sinx+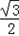 (cosx+1)=
(cosx+1)= sinx+
sinx+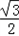 cosx+
cosx+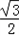 =sin(x+
=sin(x+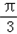 )+
)+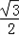 ,
,∵x+
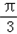 ∈(
∈(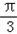 ,
,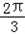 ],
],则此时函数f(x)的值域为[
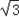 ,
,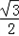 +1].
+1].
练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
