题目内容
 已知椭圆
已知椭圆| x2 |
| 8 |
| y2 |
| 2 |
(1)当m=3时,判断直线l与椭圆的位置关系(写出结论,不需证明);
(2)当m=3时,P为椭圆上的动点,求点P到直线l距离的最小值;
(3)如图,当l交椭圆于A、B两个不同点时,求证直线MA、MB与x轴始终围成一个等腰三角形.
分析:(1)当m=3时,直线l与椭圆相离.
(2)直线l的斜率为
,设直线a与直线l平行,且直线a与椭圆相切,设直线a的方程为y=
x+b…(3分)联立
,得x2+2bx+2b2-4=0…(4分),故△=(2b)2-4(2b2-4)=0,解得b=±2,由此能求出点P到直线l距离的最小值.
(3)由
,得x2+2mx+2m2-4=0,设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可.
(2)直线l的斜率为
| 1 |
| 2 |
| 1 |
| 2 |
|
(3)由
|
解答: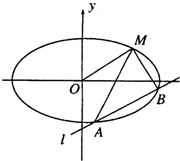 (1)解:当m=3时,直线l与椭圆相离.…(2分)
(1)解:当m=3时,直线l与椭圆相离.…(2分)
(2)解:可知直线l的斜率为
,
设直线a与直线l平行,且直线a与椭圆相切,
设直线a的方程为y=
x+b…(3分)
联立
,得x2+2bx+2b2-4=0…(4分)
∴△=(2b)2-4(2b2-4)=0,解得b=±2(5分)
∴直线a的方程为y=
x±2.
所求P到直线l的最小距离等于直线l到直线y=
x+3的距离 …(6分)
d=
=
.…(7分)
(3)证明:由
,得x2+2mx+2m2-4=0,
设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可
设A(x1,y1),B(x2,y2),且x1+x2=-2m,x1x2=2m2-4,…(9分)
而k1+k2=
+
=
…(10分)
=
=
=
…(11分)
=
=
=
=
=
=0,
∴k1+k2=0…(13分)
故直线MA、MB与x轴始终围成一个等腰三角形.…(14分)
 (1)解:当m=3时,直线l与椭圆相离.…(2分)
(1)解:当m=3时,直线l与椭圆相离.…(2分)(2)解:可知直线l的斜率为
| 1 |
| 2 |
设直线a与直线l平行,且直线a与椭圆相切,
设直线a的方程为y=
| 1 |
| 2 |
联立
|
∴△=(2b)2-4(2b2-4)=0,解得b=±2(5分)
∴直线a的方程为y=
| 1 |
| 2 |
所求P到直线l的最小距离等于直线l到直线y=
| 1 |
| 2 |
d=
| 3-2 | ||||
|
2
| ||
| 5 |
(3)证明:由
|
设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可
设A(x1,y1),B(x2,y2),且x1+x2=-2m,x1x2=2m2-4,…(9分)
而k1+k2=
| y1-1 |
| x1-2 |
| y2-1 |
| x2-2 |
| (y1-1)(x2-2)+(y2-1)(x1-2) |
| (x1-2)(x2-2) |
=
(
| ||||
| (x1-2)(x2-2) |
=
| x1x2+(m+2)(x1+x2)-4(m-1) |
| (x1-2)(x2-2) |
=
| 2m2-4+(m-2)(-2m)-4(m-1) |
| (x1-2)(x2-2) |
=
| x1x2+(m-2)(x1+x2)-4(m-1) |
| (x1-2)(x2-2) |
=
(
| ||||
| (x1-2)(x2-2) |
=
| x1x2+(m+2)(x1+x2)-4(m-1) |
| (x1-2)(x2-2) |
=
| 2m2-4+(m-2)(-2m)-4(m-1) |
| (x1-2)(x2-2) |
=
| 2m2-4-2m2+4m-4m+4 |
| (x1-2)(x2-2) |
∴k1+k2=0…(13分)
故直线MA、MB与x轴始终围成一个等腰三角形.…(14分)
点评:本题考查直线l椭圆的位置关系的判断,求点到直线距离的最小值,证明两直线与x轴始终围成一个等腰三角形.综合性强,难度大,有一定的探索性,是高考的重点.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知椭圆的中心在原点,离心率e=
,且它的一个焦点与抛物线y2=-4x的焦点重合,则此椭圆方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
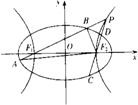 如图,已知椭圆
如图,已知椭圆