题目内容
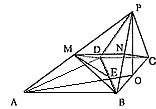
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC中点,AO交BD于E。

(1)求证:PA⊥BD;
(2)求二面角P-DC-B的大小;
(3)求证:平面PAD⊥平面PAB。
(2)求二面角P-DC-B的大小;
(3)求证:平面PAD⊥平面PAB。
(1)证明: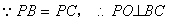 , ,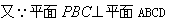 , ,平面 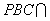 平面ABCD=BC, 平面ABCD=BC,∴PO⊥平面ABCD,  , ,∴ 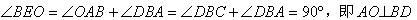 , ,∵PA在平面ABCD内的射影为AO, ∴ 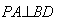 。 。(2)解:  , , ∴DC⊥平面PBC, 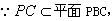 ∴ 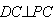 , ,∴∠PCB为二面角P-DC-B的平面角, ∵△PBC是等边三角形, ∴∠PCB=60°,即二面角P-DC-B的大小为60°。 |
|
| (3)证明:取PB的中点N,连结CN, ∵PC=BC, ∴CN⊥PB, ① ∴ 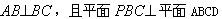 , ,∴ 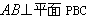 , ,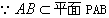 , ,∴平面PBC⊥平面PAB, ② 由①、②知CN⊥平面PAB, 连结DM、MN,则由MN∥AB∥CD, MN= 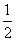 AB=CD,得四边形MNCD为平行四边形, AB=CD,得四边形MNCD为平行四边形,∴CN∥DM, ∴DM⊥平面PAB, ∵DM 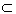 平面PAD, 平面PAD,∴平面PAD⊥平面PAB。 |
 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,