题目内容
已知:a,b,c,d∈R+,且a+b+c+d=256,则 的最大值是________.
的最大值是________.
32
分析:利用基本不等式,可得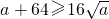 ,
,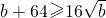 ,
,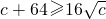 ,
,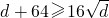 ,相加,即可得到结论.
,相加,即可得到结论.
解答:∵a,b,c,d∈R+,
∴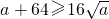 ,
,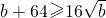 ,
,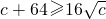 ,
,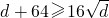
∴a+64+b+64+c+64+d+64≥16(

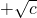
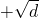 )
)
∵a+b+c+d=256,
∴512≥16(

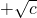
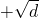 )
)
∴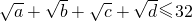 (当且仅当a=b=c=d=64时,取等号)
(当且仅当a=b=c=d=64时,取等号)
∴a=b=c=d=64时,则 的最大值是32
的最大值是32
故答案为:32
点评:本题考查函数的最值,考查基本不等式的运用,属于中档题.
分析:利用基本不等式,可得
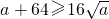 ,
,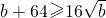 ,
,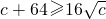 ,
,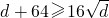 ,相加,即可得到结论.
,相加,即可得到结论.解答:∵a,b,c,d∈R+,
∴
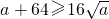 ,
,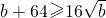 ,
,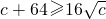 ,
,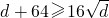
∴a+64+b+64+c+64+d+64≥16(


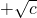
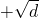 )
)∵a+b+c+d=256,
∴512≥16(


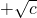
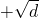 )
)∴
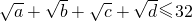 (当且仅当a=b=c=d=64时,取等号)
(当且仅当a=b=c=d=64时,取等号)∴a=b=c=d=64时,则
 的最大值是32
的最大值是32故答案为:32
点评:本题考查函数的最值,考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目