题目内容

（1）作出函数y=
sin2x
|cosx|
在两个周期的图象；
（2）作出函数y=sinx
1+cosx
1-cosx
+|cosx|，x∈(0，2π)的图象．
分析：先将函数解析式化简再作图．
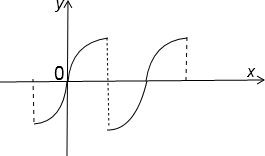
解答：解：（1）∵sin2x=2sinxcosx
∴当cosx＞0时，即-
π
2
+2kπ＜x＜
π
2
+2kπ时，y=
sin2x
|cosx|
=
2sinxcosx
cos
=2sinx
当cosx＜0时，即
π
2
+2kπ＜x＜
3π
2
+2kπ时，y=
sin2x
|cosx|
=
2sinxcosx
-cosx
=-2sinx
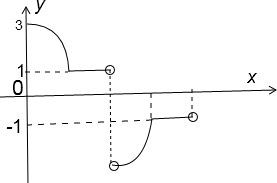
精英家教网
（2）∵y=sinx
1+cosx
1-cosx
+|cosx|=sinx•
1+cosx
|sinx|
+|cosx|
∴当x∈(0，
π
2
)时，y=1+cosx+cosx=1+2cosx
当x∈[
π
2
，π)时，y=1+cosx-cosx=1
当x∈(π，
3π
2
)时，y=-1-cosx-cosx=-1-2cosx
当x∈[
3π
2
，2π)时，y=-1-cosx+cosx=-1
精英家教网
点评：主要考查三角函数的图象．注意化简三角函数时注意分母不能是0．
练习册系列答案
相关题目
已知向量
.
m
=（cosωx，sinωx），
.
n
=（cosωx，2
3
cosωx-sinωx），ω＞0，函数f（x）=
.
m
•
.
n
+|
.
m
|，且函数f（x）图象的相邻两条对称轴之间的距离为
π
2

（1）作出函数y=f（x）-1在[0，π]上的图象
（2）在△ABC中，a，b，c分别是角A，B，C的对边，f（A）=2，c=2，S△ABC=
3
2
，求a的值．
已知函数f（x）满足f（x）+f'（0）-e-x=-1，函数g（x）=-λlnf（x）+sinx是区间[-1，1]上的减函数．
（1）当x≥0时，曲线y=f（x）在点M（t，f（t））的切线与x轴、y轴围成的三角形面积为S（t），求S（t）的最大值；
（2）若g（x）＜t2+λt+1在x∈[-1，1]时恒成立，求t的取值范围；
（3）设函数h（x）=-lnf（x）-ln（x+m），常数m∈Z，且m＞1，试判定函数h（x）在区间[e-m-m，e2m-m]内的零点个数，并作出证明．

已知向量＝(cosωx，sinωx)，＝(cosωx，2cosωx－sinωx)，ω＞0，函数f(x)＝·＋||，且函数f(x)图象的相邻两条对称轴之间的距离为

(1)作出函数y＝f(x)－1在[0，π]上的图象

(2)在△ABC中，a，b，c分别是角A，B，C的对边，f(A)＝2，c＝2，S△ABC＝，求a的值

已知函数f（x）满足f（x）+f'（0）-e-x=-1，函数g（x）=-λlnf（x）+sinx是区间[-1，1]上的减函数．
（1）当x≥0时，曲线y=f（x）在点M（t，f（t））的切线与x轴、y轴围成的三角形面积为S（t），求S（t）的最大值；
（2）若g（x）＜t2+λt+1在x∈[-1，1]时恒成立，求t的取值范围；
（3）设函数h（x）=-lnf（x）-ln（x+m），常数m∈Z，且m＞1，试判定函数h（x）在区间[e-m-m，e2m-m]内的零点个数，并作出证明．
已知向量=（cosωx，sinωx），=（cosωx，2cosωx﹣sinωx），ω＞0，函数f（x）=，且函数f（x）图象的相邻两条对称轴之间的距离为。
（1）作出函数y=f（x）﹣1在[0，π]上的图象
（2）在△ABC中，a，b，c分别是角A，B，C的对边，f（A）=2，c=2，S△ABC=，求a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网