题目内容
已知函数
，在点(1,f(1))处的切线方程为y+2=0.
(1)求函数f(x)解析式；
（2）若对于区间[-2,2]上的任意两个自变量
都有
，求实数c的最小值；
（3）若过点M（2，m）(m
2)可作曲线y=f(x)的三条切线，求实数m的取值范围；
（1）由已知得
，根据题意，得
即
解得
（2）由（1）知则
令
又f(-1)=2,f(1)=-2,f(-2)=-2,f(2)=2,
(3)设切点为（
，则
切线的斜率为
则有
，即
过点M(2,m)可作曲线y=f(x)的三条切线，方程有三个不同的实数解，
有三个不同的零点，
令
解得x=0,x=2,
练习册系列答案
相关题目
＝40；某产品的广告费用x与销售额y的统计数据如下表：
| 广告费用x(万元) | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程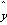
＝
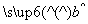x＋
中的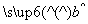为9.4，据此模型预报广告费用为6万元时销售额为( )
A．63.6万元 B．65.5万元
C．67.7万元 D．72.0万元
，且函数f(x)＝
的最小值为b，若函数g(x)＝
，则不等式g(x)≤1的解集为 ( )
B.
C.
D.
：
设
，且关于x的方程
恰有三个互不相等的实数根
，则
的取值范围是___________
（ ）
B．
C．
D．
则在这段时间内吊灯能照明的概率是（ ）
B．
C．
D．
的零点所在的大致区间是( )