题目内容
设(ax+2b)9与(bx+2a)8展开式中x3项的系数相等(a>0,b≠0)(1)求
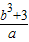 的取值范围;
的取值范围;(2)当
 展开式中二项式系数最大的项.
展开式中二项式系数最大的项.
【答案】分析:利用(ax+2b)9与(bx+2a)8展开式中x3项的系数相等,求出b与a的关系,
(1)通过基本不等式求出表达式的范围即可.
(2)通过a求出b,利用二项展开式的通项公式求出展开式最大项即可.
解答:解:(ax+2b)9展开式中x3项的系数为: .
.
(bx+2a)8展开式中x3项的系数为: .
.
则:84×24a3b6=56×25a5b3,即 .
.
(1) =
= =
= ≥2,当且仅当a=3时取等号.
≥2,当且仅当a=3时取等号.
∴ 的取值范围[2,+∞).
的取值范围[2,+∞).
(2) 时,b=1,(bx+2a)8展开式中二项式系数最大的项是第五项,
时,b=1,(bx+2a)8展开式中二项式系数最大的项是第五项,
即:T5= =70×24a4b4x4=10080x4.
=70×24a4b4x4=10080x4.
点评:本题考查二项式定理系数的形状,二项式定理的应用,考查计算能力.
(1)通过基本不等式求出表达式的范围即可.
(2)通过a求出b,利用二项展开式的通项公式求出展开式最大项即可.
解答:解:(ax+2b)9展开式中x3项的系数为:
 .
.(bx+2a)8展开式中x3项的系数为:
 .
.则:84×24a3b6=56×25a5b3,即
 .
.(1)
 =
= =
= ≥2,当且仅当a=3时取等号.
≥2,当且仅当a=3时取等号.∴
 的取值范围[2,+∞).
的取值范围[2,+∞).(2)
 时,b=1,(bx+2a)8展开式中二项式系数最大的项是第五项,
时,b=1,(bx+2a)8展开式中二项式系数最大的项是第五项,即:T5=
 =70×24a4b4x4=10080x4.
=70×24a4b4x4=10080x4.点评:本题考查二项式定理系数的形状,二项式定理的应用,考查计算能力.

练习册系列答案
相关题目
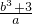 的取值范围;
的取值范围;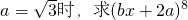 展开式中二项式系数最大的项.
展开式中二项式系数最大的项.