题目内容
如图，AC是⊙O的直径，B是圆上一点，∠ABC的平分线与⊙O相交于D，已知BC=1，AB=| 3 |
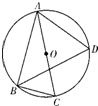
分析：由已知中AC是⊙O的直径，B是圆上一点，∠ABC的平分线与⊙O相交于D，已知BC=1，AB=
，根据圆周角定理及其推论，我们易求出圆的半径及∠AOD的度数，解△AOD即可得到答案．
| 3 |
解答：解：∵AC是⊙O的直径，B是圆上一点，
∴∠ABC=90°，
又∵BC=1，AB=
，
∴AC=2R=2，故⊙O的半径为1
又∵，∠ABC的平分线与⊙O相交于D，
∴∠ABD=45°=
∠AOD
∴∠AOD=90°
∴AD=
故答案为：
∴∠ABC=90°，
又∵BC=1，AB=
| 3 |
∴AC=2R=2，故⊙O的半径为1
又∵，∠ABC的平分线与⊙O相交于D，
∴∠ABD=45°=
| 1 |
| 2 |
∴∠AOD=90°
∴AD=
| 2 |
故答案为：
| 2 |
点评：本题考查的知识点是圆周角定理及其推论，勾股定理，其中根据圆周角定理及其推论，求出圆的半径及∠AOD的度数，是解答本题的关键．
练习册系列答案
相关题目
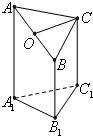如图是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC．已知A1B1=B1C1=1，∠A1B1C1=90°，AA1=4，BB1=2，CC1=3．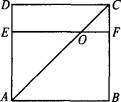
与直线
的夹角大小为
B．（不等式选讲）要使关于x的不等式
在实数