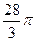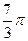题目内容
设地球是半径为R的球,地球上A、B两地都在北纬45°的纬线上,A在
东经20°、B在东经110°的经线上,则A、B两地的球面距离是 ( )
A. B.
B. C.
C. D.
D.
C
解析考点:球面距离及相关计算.
专题:计算题.
分析:A、B两地在同一纬度圈上,计算经度差,求出AB弦长,以及球心角,然后求出球面距离.
解答:解:地球表面上从A地(北纬45°,东经20°)到B地(北纬45°,东经110°)
AB的纬圆半径是  ,经度差是90°,
,经度差是90°,
所以AB=R
球心角是  ,
,
A、B两地的球面距离是 
故选C.
点评:本题考查球面距离及其他计算,考查空间想象能力,是基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
如图,已知正方体 的棱长为
的棱长为 ,点
,点 在线段
在线段 上,点
上,点 在线段
在线段 上,点
上,点 在线段
在线段 上,且
上,且 ,
, ,
, ,
, 是
是 的中点,则四面体
的中点,则四面体 的体积( )
的体积( )
A.与 有关,与 有关,与 无关 无关 | B.与 无关,与 无关,与 无关 无关 |
C.与 无关,与 无关,与 有关 有关 | D.与 有关,与 有关,与 有关 有关 |
在四面体S—ABC中, ,二面角S—AC—B的余弦值是
,二面角S—AC—B的余弦值是 ,则该四面体外接球的表面积是 ( )
,则该四面体外接球的表面积是 ( )
A. | B. | C.24 | D.6 |
两个球体积之和为12π,且这两个球的球大圆周长之和 为6π,那么这两球半径之差是
为6π,那么这两球半径之差是
A. | B.1 | C.2 | D.3 |
一个与球心距离为1的平面截球所得的圆面积为 ,则球的表面积为( )
,则球的表面积为( )
A. | B. | C. | D. |




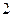 和
和 ,腰长为
,腰长为 的等腰梯形,则该几何体的体积是 ( )
的等腰梯形,则该几何体的体积是 ( )