题目内容
函数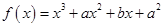 在
在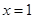 时有极值10,则
时有极值10,则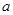 的值为( )
的值为( )
| A.-3或4 | B.4 | C.-3 | D.3或 4 |
B
解析试题分析:对函数f(x)求导得 f′(x)=3x2+2ax+b,又∵在x=1时f(x)有极值10,∴f′(1)=3+2a+b=0 f(1)=1+a+b+a2=10,解得 a=4,b=-11 或 a=-3,b=3,当a=-3,b=3时,在x=1时f(x)无极值;当a=4,b=-11 符合题意.故选:B.
考点:函数在某点取得极值的条件.

练习册系列答案
相关题目
已知函数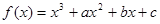 有两个极值点
有两个极值点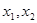 ,若
,若 ,则关于
,则关于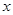 的方程
的方程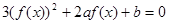 的不同实根个数为 ( )
的不同实根个数为 ( )
| A.3 | B.4 | C.5 | D.6 |
已知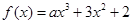 ,若
,若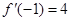 ,则
,则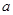 的值等于 ( )
的值等于 ( )
A.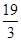 | B.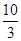 | C.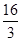 | D.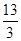 |
已知函数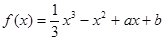 ,
,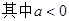 ,如果存在实数
,如果存在实数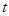 ,使
,使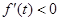 ,则
,则 的值( )
的值( )
| A.必为正数 | B.必为负数 | C.必为非负 | D.必为非正 |
过曲线 上的点
上的点 的切线平行于直线
的切线平行于直线 ,则切点
,则切点 的坐标为( )
的坐标为( )
A. 或 或 | B. 或 或 |
C. 或 或 | D. 或 或 |
函数y= x2
x2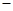 ㏑x的单调递减区间为( )
㏑x的单调递减区间为( )
A.(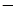 1,1] 1,1] | B.(0,1] | C.[1,+∞) | D.(0,+∞) |
函数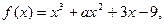 已知
已知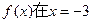 时取得极值,则
时取得极值,则 的值等于( )
的值等于( )
| A.2 | B.3 | C.4 | D.5 |
若f(x)=2lnx﹣x2,则f′(x)>0的解集为( )
| A.(0,1) |
| B.(﹣∞,﹣1)∪(0,1) |
| C.(﹣1,0)∪(1,+∞) |
| D.(1,+∞) |
某银行准备新设一种定期存款业务,经预测,存款量与存款利率成正比,比例系数为k(k>0),贷款的利率为4.8%,假设银行吸收的存款能够全部贷出去.若存款利率为x(x∈(0,0.048)),则银行可获得最大收益时,存款利率为 ( )
| A.0.03 |
| B.0.024 |
| C.0.02 |
| D.0.016 |