题目内容
已知点A(1,1)是椭圆 上一点,F1,F2是椭圆的两焦点,且满足|AF1|+|AF2|=4.
上一点,F1,F2是椭圆的两焦点,且满足|AF1|+|AF2|=4.
(I)求椭圆的两焦点坐标;
(II)设点B是椭圆上任意一点,如果|AB|最大时,求证A、B两点关于原点O不对称.
解:(I)由椭圆定义知:2a=4,
∴a=2
∴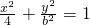
把(1,1)代入得
∴
∴
故两焦点坐标 为 .…(3分)
.…(3分)
(II)用反证法:假设A、B两点关于原点O对称,则B点坐标为(-1,-1),
此时
取椭圆上一点
∴|AM>|AB|.
从而此时|AB|不是最大,这与|AB|最大矛盾,所以命题成立. …(7分)
分析:(I)由椭圆定义知:2a=4,把(1,1)代入得 求出b,根据
求出b,根据 进一步求出两焦点坐标.
进一步求出两焦点坐标.
(II)用反证法:假设A、B两点关于原点O对称,则B点坐标为(-1,-1),此时 ;再取椭圆上一点
;再取椭圆上一点 得到|AM>|AB|.即得证.
得到|AM>|AB|.即得证.
点评:本题考查椭圆的定义及椭圆中三个参数的关系:c2=a2-b2;考查利用反证法证明命题,属于中档题.
∴a=2
∴
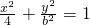
把(1,1)代入得

∴

∴

故两焦点坐标 为
 .…(3分)
.…(3分)(II)用反证法:假设A、B两点关于原点O对称,则B点坐标为(-1,-1),
此时

取椭圆上一点

∴|AM>|AB|.
从而此时|AB|不是最大,这与|AB|最大矛盾,所以命题成立. …(7分)
分析:(I)由椭圆定义知:2a=4,把(1,1)代入得
 求出b,根据
求出b,根据 进一步求出两焦点坐标.
进一步求出两焦点坐标.(II)用反证法:假设A、B两点关于原点O对称,则B点坐标为(-1,-1),此时
 ;再取椭圆上一点
;再取椭圆上一点 得到|AM>|AB|.即得证.
得到|AM>|AB|.即得证.点评:本题考查椭圆的定义及椭圆中三个参数的关系:c2=a2-b2;考查利用反证法证明命题,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (a>b>0)上一点,F1,F2是椭圆的两焦点,且满足|AF1|+|AF2|=4.
(a>b>0)上一点,F1,F2是椭圆的两焦点,且满足|AF1|+|AF2|=4.