题目内容
已知函数f(x)=a1x+a2x2+a3x3+…+anxn(n∈N*),且a1,a2,a3,…,an构成一个数列,又f(1)=n2,(1)求数列{an}的通项公式;
(2)求证:f(![]() )<1.
)<1.
思路解析:从f(1)=n2知,数列{an}的前n项和Sn=n2,这样,就将问题转化为“知Sn求an”的问题了. 解:(1)在f(x)中,令x=1,则f(1)=a1+a2+a3+…+an, ∵ f(1)=n2,∴ a1+a2+a3+…+an=n2,即Sn=n2. 当n=1时,a1=S1=1, 当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1. 验证知,a1=1也适合上式,∴ an=2n-1(n∈N*). (2)∵ f( ∴ 两式相减,得 = ∴ f( 评注:此题综合了数列与函数,数列与不等式,及数列求和等多方面的知识,值得研究.![]() )=
)=![]() +3×(
+3×(![]() )2+5×(
)2+5×(![]() )3+…+(2n-1)×(
)3+…+(2n-1)×(![]() )n,
)n,![]() f(
f(![]() )=1×(
)=1×(![]() )2+3×(
)2+3×(![]() )3+…+(2n-3)×(
)3+…+(2n-3)×(![]() )n+(2n-1)×(
)n+(2n-1)×(![]() )n+1.
)n+1.![]() f(
f(![]() )=
)=![]() +2[(
+2[(![]() )2+(
)2+(![]() )3+…+(
)3+…+(![]() )n]-(2n-1)×(
)n]-(2n-1)×(![]() )n+1
)n+1![]() +2×
+2×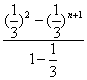 -(2n-1)×(
-(2n-1)×(![]() )n+1=
)n+1=![]() -2(n+1)(
-2(n+1)(![]() )n+1,
)n+1,![]() )=1-(n+1)(
)=1-(n+1)(![]() )n<1.
)n<1.
直接高考Sunny假期作业
阳光出版社系列答案
暑假总动员宁夏人民教育出版社系列答案
鑫浪传媒给力100暑假作业系列答案
骄子之路暑假作业河北人民出版社系列答案
Happy holiday快乐假期暑假作业延边教育出版社系列答案
假期总动员四川师范大学电子出版社系列答案
暑假训练营学年总复习希望出版社系列答案
滴水穿石初中暑假快乐提升晨光出版社系列答案
暑假作业本浙江教育出版社系列答案
学习与探究暑假学习系列答案