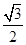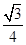题目内容
在海岸A处,发现北偏东45°方向、距离A处( -1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10
-1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10 海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
 -1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10
-1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10 海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?缉私船沿北偏东60°的方向能最快追上走私船,最少要花 小时.
小时.
 小时.
小时.如图,设缉私船t小时后在D处追上走私船,

则有CD=10 t,BD=10t.
t,BD=10t.
在△ABC中,AB= -1,AC=2,∠BAC=120°.
-1,AC=2,∠BAC=120°.
利用余弦定理可得BC= .
.
由正弦定理,得
sin∠ABC= sin∠BAC=
sin∠BAC= ×
× =
= ,
,
得∠ABC=45°,即BC与正北方向垂直.
于是∠CBD=120°.
在△BCD中,由正弦定理,得
sin∠BCD= =
= =
= ,
,
得∠BCD=30°,∴∠BDC=30°.
又 =
= ,
,
 =
= ,得t=
,得t= .
.
所以缉私船沿北偏东60°的方向能最快追上走私船,最少要花 小时.
小时.

则有CD=10
 t,BD=10t.
t,BD=10t.在△ABC中,AB=
 -1,AC=2,∠BAC=120°.
-1,AC=2,∠BAC=120°. 利用余弦定理可得BC=
 .
.由正弦定理,得
sin∠ABC=
 sin∠BAC=
sin∠BAC= ×
× =
= ,
,得∠ABC=45°,即BC与正北方向垂直.
于是∠CBD=120°.
在△BCD中,由正弦定理,得
sin∠BCD=
 =
= =
= ,
,得∠BCD=30°,∴∠BDC=30°.
又
 =
= ,
, =
= ,得t=
,得t= .
.所以缉私船沿北偏东60°的方向能最快追上走私船,最少要花
 小时.
小时.
练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
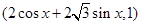 ,n=
,n=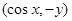 ,满足
,满足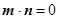 .
. ,并求
,并求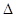 ABC的三个内角A,B,C对应的边长,
ABC的三个内角A,B,C对应的边长,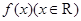 的最大值是
的最大值是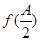 ,且a=2,求b+c的取值范围.
,且a=2,求b+c的取值范围.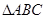 中,角
中,角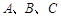 所对的边分别为
所对的边分别为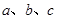 ,已知
,已知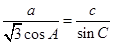 ,
,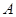 的大小;(2)若
的大小;(2)若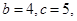 求
求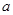 的值.
的值. 的三内角
的三内角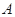 、
、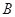 、
、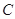 所对边的边长分别为
所对边的边长分别为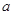 、
、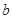 、
、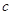 ,且
,且 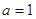 ,
,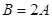 ,则
,则
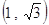
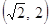
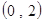
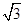 ,则c等于( )
,则c等于( )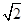 (D)1
(D)1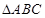 中,角
中,角 、
、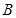 、
、 所对的边分别为
所对的边分别为 、
、 、
、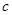 ,若
,若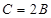 ,则
,则 为( )
为( )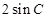


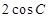
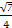 (其中C为锐角).
(其中C为锐角). ,C=
,C= ,则S△ABC=________.
,则S△ABC=________.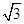 ,AC=1,B=
,AC=1,B=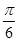 ,则△ABC的面积为( ).
,则△ABC的面积为( ).