题目内容
已知函数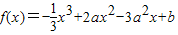 ,(a,b∈R)
,(a,b∈R)(1)当a=3时,若f(x)有3个零点,求b的取值范围;
(2)对任意
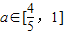 ,当x∈[a+1,a+m]时恒有-a≤f'(x)≤a,求m的最大值,并求此时f(x)的最大值.
,当x∈[a+1,a+m]时恒有-a≤f'(x)≤a,求m的最大值,并求此时f(x)的最大值.
【答案】分析:(1)把a=3代入f(x),函数f(x)进行求导,求出函数单调区间,研究其极值,从而求出b的范围;
(2)对任意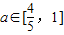 ,可知当x∈[a+1,a+m]时恒有-a≤f'(x)≤a,将问题转化为f'(a+1)=2a-1<a恒成立,再利用常数分离法进行求解;
,可知当x∈[a+1,a+m]时恒有-a≤f'(x)≤a,将问题转化为f'(a+1)=2a-1<a恒成立,再利用常数分离法进行求解;
解答:解:∵函数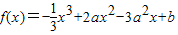 ,
,
∴f'(x)=-x2+4ax-3a2
(1)若a=3,f'(x)=-(x-3)(x-9),
f(x)极小值=f(3)=-36+b,
f(x)极大值=f(9)=b
由题意: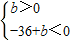
∴0<b<36
(2)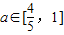 时,有2a≤a+1≤2,
时,有2a≤a+1≤2,
由f'(x)图象,f'(x)在[a+1,a+m]上为减函数,
∴f'(a+m)<f'(a+1)易知f'(a+1)=2a-1<a必成立;
只须f'(a+m)≥-a得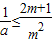
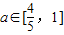 ,
,
可得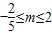
又m>1,
∴1<m≤2m最大值为2
此时x∈[a+1,a+2],有2a≤a+1<3a≤a+2,
∴f(x)在[a+1,3a]内单调递增,在[3a,a+2]内单调递减,
∴f(x)max=f(3a)=b;
点评:此题主要考查利用导数研究函数的单调性及其应用,这类题型是高考的热点问题,是一道中档题;
(2)对任意
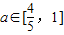 ,可知当x∈[a+1,a+m]时恒有-a≤f'(x)≤a,将问题转化为f'(a+1)=2a-1<a恒成立,再利用常数分离法进行求解;
,可知当x∈[a+1,a+m]时恒有-a≤f'(x)≤a,将问题转化为f'(a+1)=2a-1<a恒成立,再利用常数分离法进行求解;解答:解:∵函数
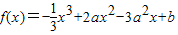 ,
,∴f'(x)=-x2+4ax-3a2
(1)若a=3,f'(x)=-(x-3)(x-9),
f(x)极小值=f(3)=-36+b,
f(x)极大值=f(9)=b
由题意:
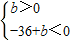
∴0<b<36
(2)
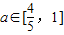 时,有2a≤a+1≤2,
时,有2a≤a+1≤2,由f'(x)图象,f'(x)在[a+1,a+m]上为减函数,
∴f'(a+m)<f'(a+1)易知f'(a+1)=2a-1<a必成立;
只须f'(a+m)≥-a得
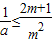
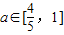 ,
,可得
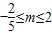
又m>1,
∴1<m≤2m最大值为2
此时x∈[a+1,a+2],有2a≤a+1<3a≤a+2,
∴f(x)在[a+1,3a]内单调递增,在[3a,a+2]内单调递减,
∴f(x)max=f(3a)=b;
点评:此题主要考查利用导数研究函数的单调性及其应用,这类题型是高考的热点问题,是一道中档题;

练习册系列答案
相关题目
 已知函数
已知函数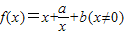 ,其中a,b∈R.
,其中a,b∈R.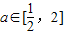 ,不等式f(x)≤10在
,不等式f(x)≤10在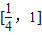 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.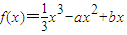 .(a,b∈R)
.(a,b∈R) ,其中a,b∈R.
,其中a,b∈R. ,不等式f(x)≤10在
,不等式f(x)≤10在 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.