题目内容
已知向量a,b满足|a|=|b|=2,a?b=0，若向量c与a-b共线，则|a+c|的最小值为（ ）
| A．1 | B． | C． | D．2 |
B
解析
如图,设
="b," 
=a,则
=a-b
作CD⊥AB于D
∵向量c与a-b共线
|a+c|的最小值即为|
|=
练习册系列答案
相关题目
已知向量
满足
，则向量夹角的余弦值为 （ ）
A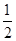． | B． | C． | D． |
下列结论中，正确结论的个数是（ ）
（1）若
，且
，则
（2）
（3）
（4）若
,
,
，
，
则
或
| A．0 | B．1 | C．2 | D．3 |
已知向量
，
，且
，则y取最小值时，向量
在
方向上的投影为（ ）
A． | B． | C． | D． |
若四边形ABCD满足
＋
＝0，(－
)·
＝0，则该四边形一定是( )
| A．直角梯形 | B．菱形 | C．矩形 | D．正方形 |
＋μ
，则λ＋μ＝( )
B.
C.
D.
已知向量
=（3，0），
=（0，1），若
与
共线，则实数的λ值为（ ）
| A．1 | B．﹣1 | C． | D． |
已知向量a、b的夹角为45°，且|a|＝1，|2a－b|＝
，则|b|＝( )
A．3 | B．2 | C． | D．1 |