题目内容
若直线y=x+b与曲线y=1+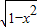
有两个不同的公共点，则实数b的取值范围为 ．
【答案】分析：曲线表示以C（0，1）为圆心、半径等于1的半圆，当直线y=x+b过点（0，2）时，可得b=2，满足条件．当直线y=x+b和半圆相切时，由1=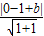
解得 b=1+
，
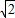数形结合可得实数b的取值范围．
解答：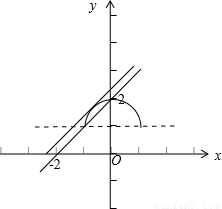
解：曲线y=1+
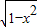即 x2+（y-1）2=1 （y≥1），表示以C（0，1）为圆心、半径等于1的半圆，如图所示：
当直线y=x+b过点（0，2）时，可得b=2，满足直线y=x+b与曲线y=1+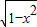
有两个不同的公共点．
当直线y=x+b和半圆相切时，由1=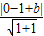
解得 b=1+
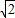，或b=1-
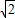（舍去），
故直线y=x+b与曲线y=1+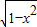
有两个不同的公共点时，实数b的取值范围为[2，1+
），
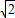故答案为[2，1+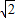
）．
点评：本题主要考查直线和圆相交的性质，点到直线的距离公式的应用，体现了数形结合的数学思想，属于中档题．
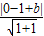解得 b=1+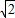，数形结合可得实数b的取值范围．
解答：
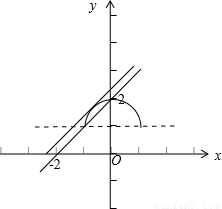解：曲线y=1+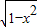即 x2+（y-1）2=1 （y≥1），表示以C（0，1）为圆心、半径等于1的半圆，如图所示：当直线y=x+b过点（0，2）时，可得b=2，满足直线y=x+b与曲线y=1+
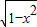有两个不同的公共点．当直线y=x+b和半圆相切时，由1=
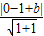解得 b=1+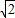，或b=1- 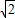（舍去），故直线y=x+b与曲线y=1+
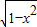有两个不同的公共点时，实数b的取值范围为[2，1+ 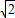），故答案为[2，1+
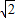）．点评：本题主要考查直线和圆相交的性质，点到直线的距离公式的应用，体现了数形结合的数学思想，属于中档题．
练习册系列答案
相关题目
，|AN|＝3，且|BN|＝6，分别以l1及l2为x轴和y轴，建立如图坐标系，求曲线C的方程．
)为圆心，1为半径的圆相切，又知C的一个焦点与A关于y = x对称．
，+∞]
）
，+∞]
）