题目内容
已知数列{an}是等差数列,a2=3,a4+a5+a6=27,Sn为数列{an}的前n项和
(1)求an和Sn;
(2)若 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
解:(1)由已知a4+a5+a6=27,可得3a5=27,
解得a5=9.(1分)
设等差数列{an}的公差为d,则a5-a2=3d=6,解得d=2..(2分)
∴an=a2+(n-2)d=3+(n-2)×2=2n-1,(4分)
故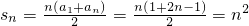 ,
,
综上,an=2n-1,sn=n2(7分)
(2)把an=2n-1代入得 =
=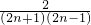 =
= -
- ,
,
所以Tn=b1+b2+…+bn=(1- )+(
)+( -
- )+…(
)+…( -
- )=1-
)=1- =
= .
.
分析:(1)根据等差数列的性质化简a4+a5+a6=27,即可求出a5的值,又a2和a5的值,再利用等差数列的性质即可求出公差d的值,进而由a2和公差d写出通项公式及前n项和即可;
(2)把(1)求出的an的通项公式代入到bn中,化简可得bn的通项公式,列举出数列{bn}的各项,抵消后即可求出数列{bn}的前n项和Tn.
点评:此题考查学生灵活运用等差数列的性质化简求值,灵活运用等差数列的通项公式及前n项和公式化简求值,是一道中档题.
解得a5=9.(1分)
设等差数列{an}的公差为d,则a5-a2=3d=6,解得d=2..(2分)
∴an=a2+(n-2)d=3+(n-2)×2=2n-1,(4分)
故
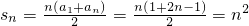 ,
,综上,an=2n-1,sn=n2(7分)
(2)把an=2n-1代入得
 =
=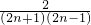 =
= -
- ,
,所以Tn=b1+b2+…+bn=(1-
 )+(
)+( -
- )+…(
)+…( -
- )=1-
)=1- =
= .
.分析:(1)根据等差数列的性质化简a4+a5+a6=27,即可求出a5的值,又a2和a5的值,再利用等差数列的性质即可求出公差d的值,进而由a2和公差d写出通项公式及前n项和即可;
(2)把(1)求出的an的通项公式代入到bn中,化简可得bn的通项公式,列举出数列{bn}的各项,抵消后即可求出数列{bn}的前n项和Tn.
点评:此题考查学生灵活运用等差数列的性质化简求值,灵活运用等差数列的通项公式及前n项和公式化简求值,是一道中档题.

练习册系列答案
相关题目