Question

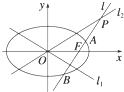已知椭圆C的方程为

x2

a2

+

y2

b2

=1（a＞b＞0），双曲线

x2

a2

-

y2

b2

=1的两条渐近线为l₁、l₂，过椭圆C的右焦点F作直线l，使l⊥l₁，又l与l₂交于P点，设l与椭圆C的两个交点由上至下依次为A、B．（如图）
（1）当l₁与l₂夹角为60°，双曲线的焦距为4时，求椭圆C的方程；
（2）当

FA

=λ

AP

时，求λ的最大值．

Answer 1

分析：（1）要求椭圆方程即求a、b的值，根据l₁与l₂的夹角为60°可以得

b

a

=

3

3

，由双曲线的距离为4可以得a²+b²=4，进而解关于a，b的方程组可以得a、b，写出椭圆的标准方程．
（2）根据

FA

=λ

AP

，欲求λ的最大值，需求A、P的坐标，而P是l与l₁的交点，故需求l的方程．将l与l₂的方程联立可求得P的坐标，进而可求得点A的坐标．将A的坐标代入椭圆方程可求得λ的最大值．

解答：解：（1）∵双曲线的渐近线为y=±

b

a

x，两渐近线夹角为60°，
又

b

a

＜1，∴∠POx=30°，即

b

a

=tan30°=

3

3

．
∴a=

3

b．
又a²+b²=4，
∴a²=3，b²=1．
故椭圆C的方程为

x2

3

+y²=1．
（2）由已知l：y=

a

b

（x-c），与y=

b

a

x解得P（

a2

c

，

ab

c

），
由

FA

=λ

AP

得A（

c+λ• a2 c

1+λ

，

λ• ab c

1+λ

）．
将A点坐标代入椭圆方程得（c²+λa²）²+λ²a⁴=（1+λ）²a²c²．
∴（e²+λ）²+λ²=e²（1+λ）²．
∴λ²=

e4-e2

e2-2

=-[（2-e²）+

2

2-e2

]+3≤3-2

2

．
∴λ的最大值为

2

-1．

点评：本题考查圆锥曲线的共同特征，考查椭圆的标准方程，考查双曲线的应用，考查函数的最值，本题是一个综合题目．