题目内容
已知抛物线y2=-4x上的焦点F,点P在抛物线上,点A(-2,1),则要使|PF|+|PA|的值最小的点P的坐标为
- A.

- B.
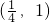
- C.

- D.

A
分析:利用抛物线的定义,将点P(m,n)到焦点F的距离|PF|转化为它到准线l:x=1的距离,利用不等式即可求得答案.
解答:∵抛物线y2=-4x的焦点F,
∴F(-1,0),其准线方程为l:x=1;
∵点P在抛物线上,点A(-2,1),
设点P在准线l:x=1上的射影为P′,
则|PF|=|PP′|,
∴|PF|+|PA|=|PA|+|PP′|≥|AP′|=3(当A,P,P′三点共线时取“=”).
此时P点的纵坐标为n=1,
由12=-4m得:m=- .
.
∴点P的坐标为(- ,1).
,1).
故选A.
点评:本题考查抛物线的简单性质,考查转化思想与不等式思想,属于中档题.
分析:利用抛物线的定义,将点P(m,n)到焦点F的距离|PF|转化为它到准线l:x=1的距离,利用不等式即可求得答案.
解答:∵抛物线y2=-4x的焦点F,
∴F(-1,0),其准线方程为l:x=1;
∵点P在抛物线上,点A(-2,1),
设点P在准线l:x=1上的射影为P′,
则|PF|=|PP′|,
∴|PF|+|PA|=|PA|+|PP′|≥|AP′|=3(当A,P,P′三点共线时取“=”).
此时P点的纵坐标为n=1,
由12=-4m得:m=-
 .
.∴点P的坐标为(-
 ,1).
,1).故选A.
点评:本题考查抛物线的简单性质,考查转化思想与不等式思想,属于中档题.

练习册系列答案
相关题目